ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ
.. 2
ГЛАВА 1. ГРУППЫ И ИХ ОБРАЗУЮЩИЕ
.. 5
1.1. Основные понятия группы
.. 5
1.1.1. Алгебраическая операция
. 5
1.1.2. Группа
. 6
1.2. Образующие элементы группы. Система образующих
. 13
1.2.1. Понятие образующего элемента
. 13
1.2.2. Система образующих. Конечное число образующих
. 14
1.2.3. Непорождающие элементы
.. 19
1.3. Циклические группы
.. 21
1.3.1. Подгруппа, порожденная данным элементом данной группы. Определение циклической группы
.. 21
ГЛАВА 2. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ГРУПП
.. 26
2.1. Граф группы
.. 27
2.1.1. Бесконечная циклическая группа
. 30
2.1.2. Группа с двумя образующими
. 31
2.2. Основные свойства графа группы
.. 33
ЛИТЕРАТУРА
.. 38
ВВЕДЕНИЕ
Исследование алгебраических уравнений в начале XIX века привело математиков к необходимости выделения особого математического понятия — понятия группы. Новое понятие оказалось настолько плодотворным, что не только проникло почти во все разделы современной математики, но и стало играть важную роль в некоторых разделах других наук, например, в квантовой механике и в кристаллографии. Исследования, связанные с понятием группы, выросли в отдельную ветвь современной математики — теорию групп. Что же представляет собой понятие группы в математике? Какой смысл несут образующие элементы в группе? Что такое система образующих? На эти и другие вопросы предстоит ответить в данной работе.
Работа посвящена рассмотрению и описанию образующих элементов в теории групп. Группа — один из основных типов алгебраических систем, а теория групп — один из основных разделов современной алгебры.
В настоящее время теория групп является одной из самых развитых областей алгебры, имеющих многочисленные применения как в самой математики, так и за ее пределами — в топологии, теории функции, кристаллографии, квантовой механике и других областях математики и естествознания. Конечной целью собственно теории групп является описание всех групповых композиций.
Понятие же группы приобретает в настоящее время все большее господство над самыми различными разделами математики и ее приложений и наряду с понятием функции относится к самым фундаментальным понятиям всей математики.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
Образующие элементы в группе — это базовое понятие теории. Элементы эти можно сравнить с буквами, из которых состоят слова. Отсюда делаем вывод, что изучение темы: «Образующие элементы» — имеет практическое и теоретическое значение, а в следствии этого актуальным на сегодняшний день…
Целью данной работы является рассмотрение образующих элементов в различных группах, а также описание того, как ведут себя образующие элементы и системы образующих в тех или иных группах.
А для достижения поставленной в курсовой работе цели нами решались следующие задачи:
— рассмотрение основных определений группы: алгебраической операции, понятие группы, циклической группы
— определение сущности понятия образующих элементов
— рассмотрение систем образующих элементов
— введение понятия непорождающих элементов
— анализ поведения образующих элементов в различных группах
— рассмотрение графического описания групп и др.
Объектом исследования в работе являются группы различных видов, а соответственно, предметом исследования являются образующие элементы группы. Так как образующий элемент — это одно из основных понятий группы, следовательно, предмет исследования является частью объекта исследования.
Опишем вкратце содержание.
Глава 1 посвящена изучению основных понятий группы. Содержит все необходимые для дальнейшего изучения сведения из теории групп. Здесь же вводится понятие образующего элемента, а также системы образующих. Кроме того, приводится большое количество наглядных примеров групп различных видов с различными элементами, в том числе и циклических групп.
Известно, что геометрическим эквивалентом групп являются графы. Вторая глава работы полностью посвящена графическому представлению групп, т.е. графам. Здесь будут рассмотрены подробные примеры различных групп, представленных графами, а именно конечные и бесконечные группы, а также некоторые свойства графов. Кроме того, в этой главе мы узнаем, что ставится в соответствие в графе элементам и образующим группы, и каковы образующие элементы конечных и бесконечных групп.
Глава 3 — это практическая часть курсовой работы. Здесь приводится ряд основных задач и упражнений, посвященных теме «образующие элементы».
Курсовое исследование написано при использовании литературы по теории групп, комбинаторной теории групп, основам алгебры, введению в теорию групп, группам и их графам. Кроме того, использовались интернет-ресурсы. Библиографический список представлен в конце курсовой работы.
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
Список литературы, используемой в данной работе, можно рекомендовать для изучения других проблем, не освещенных в данной курсовой работе.
ГЛАВА 1. ГРУППЫ И ИХ ОБРАЗУЮЩИЕ
1.1. Основные понятия группы
1.1.1. Алгебраическая операция
Весьма часто <…> в различных приложениях встречаются множества, в которых определена (или в данный момент рассматривается) лишь одна алгебраическая операция. Дадим определение этого понятия.
Определение
Пусть дано некоторое множество М.
Мы говорим, что в М
определена бинарная алгебраическая операция
, если всяким двум (различным или одинаковым) элементам множества М
,взятым в определенном порядке, по некоторому закону ставится в соответствие вполне определенный третий элемент, принадлежащий к этому же множеству[1]
).
Требование однозначности операции и требование ее выполнимости для любой пары элементов входят, следовательно, в определение алгебраической операции. С другой стороны, в этом определении содержится указание на порядок, в котором берутся элементы множества М
при выполнении операции. Иными словами, не исключается возможность того, что паре элементов а
,b
из М
и паре b
, а
будут поставлены в соответствие различные элементы из М,
т.е. что рассматриваемая операция будет некоммутативной
.
Примеры
Можно указать многочисленные примеры числовых множеств с одной операцией, удовлетворяющих данному выше определению. Бинарными операциями являются, например, сложение на множестве натуральных или на множестве целых чисел, вычитание на множестве целых чисел.
Этому определению не удовлетворяют, например, вычитание на множестве натуральных чисел, т.к., например, упорядоченной паре (3, 5) вычитание не ставит в соответствие никакого натурального числа, множество отрицательных целых чисел относительно умножения, множество нечетных чисел относительно сложения, а также множество всех действительных чисел, если в качестве операции рассматривается деление — последнее ввиду невыполнимости деления на нуль.
Хорошо известны также различные примеры алгебраических операций, производимых не над числами. Таковы сложение n
-мерного векторного пространства, векторное умножение трехмерного евклидова пространства, умножение квадратных матриц порядка n
, сложение действительных функций действительного переменного, умножение этих же функций и т.д. Примером алгебраической операции также является умножение подстановок
.
<…>
При изучении множеств с одной алгебраической операцией мы будем, как правило, употреблять мультипликативную терминологию и символику: операцию будем называть умножением
,а результат применения операции к паре элементов а,
b
— произведением
а
b
этих элементов. В некоторых случаях будет удобнее, однако, использовать аддитивную запись, т.е. называть операцию сложением
и говорить о сумме
а
+ b
элементов а,
b
.[2]
1.1.2. Группа
Дадим теперь общее определение группы.
Определение 1
Группой
называется множество G
элементов а
, b
, ..., для которых определена некоторая алгебраическая операция (обычно называемая умножением или сложением), ставящая в соответствие каждой упорядоченной паре a
, b
элементов из G
третий элемент с
= а
º b
, причем так, что выполнены следующие условия (аксиомы):
1. Эта операция ассоциативна
: для любых трех элементов а,
b
, с из
G
:
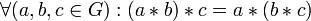 . .
2. ВG
существует «нейтральный»
элемент е
такой, что:
 .
.
3. Для каждого элемента а
из G
существует «обратный»
ему элемент а
–1
такой, что:
 .
.
Группа, в которой дополнительно выполняется коммутативный закон:
для любых двух элементов а
, b
ÎG
а
° b
= b
° а
, называется коммутативной, или абелевой
(по имени Абеля, изучавшего один тип уравнений, теория которых связана с теорией коммутативных групп). Операция в группе G
не обязана быть коммутативной. <…>
Группа, состоящая из конечного числа элементов, называется конечной группой. Число элементов конечной группы называется ее порядком
. Группа, не являющаяся конечной, называется бесконечной
.
В том случае, когда «групповая операция» а
° b
называется сложением и обозначается знаком +, группа G
называется группой по сложению
,
или аддитивной группой
.
В этом случае «нейтральный элемент» е
обычно обозначается символом 0 и называется нулем
,
а элемент, обратный к а,
обозначается через — а
–1
и называется противоположным
к а
. В том случае, когда групповая операция называется умножением, а ° b
обозначается через ab
, группа называется группой по умножению
,
или мультипликативной группой
,
а нейтральный элемент называется единицей
и часто обозначается символом 1.[3]
Комментарии к определению группы
1. Элемент а
–1
, обратный элементу a
, единственен.
2. В определении группы 2-ю и 3-ю аксиомы можно заменить одной аксиомой существования обратной операции:
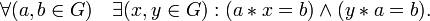
3. Вышеприведенные аксиомы не являются строго минимальными. Для существования нейтрального и обратного элементов достаточно наличия левого нейтрального (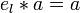 ) и левого обратного ( ) и левого обратного (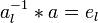 ) элементов. При этом они автоматически являются e
и а
–1
:[4] ) элементов. При этом они автоматически являются e
и а
–1
:[4]
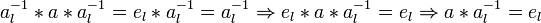 . .
Свойства группы
1. Элемент а
–1
, обратный элементу a
, всегда определяется однозначно.
Доказательство
В самом деле, если элементы y
и z
являются обратными для a
, то y
*x
= e
и z
*x
= e
, откуда y
*x
= z
*x
и по закону сокращения y
= z
.
2. Верны законы сокращения:
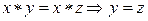 (левое сокращение); (левое сокращение);
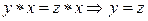 (правое сокращение). (правое сокращение).
Доказательство
Докажем первый закон. Используем существование обратного элемента 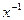 и свойство ассоциативности операции. и свойство ассоциативности операции.
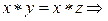
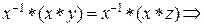
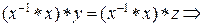
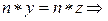 y= z. Что и требовалось доказать. Второй закон (для правого сокращения) доказывается анологично. y= z. Что и требовалось доказать. Второй закон (для правого сокращения) доказывается анологично.
3. Обратный элемент к нейтральному есть сам нейтральный элемент.
Доказательство
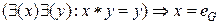 . .
Действительно, поскольку 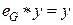 , имеем , имеем 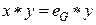 , откуда по закону сокращения получаем , откуда по закону сокращения получаем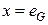 . .
4. Для любых x
, y
уравнение вида x
*z
= y
имеет единственное решение, равное 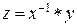 . Оно называется частным от деления y
на x
(или отношением элементов y
и x
) и обозначается y
/
x
. . Оно называется частным от деления y
на x
(или отношением элементов y
и x
) и обозначается y
/
x
.
Доказательство
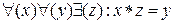 . Имеем: . Имеем: 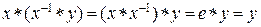 , и значит можно взять , и значит можно взять 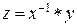 . Однозначность z
следует из закона сокращения: . Однозначность z
следует из закона сокращения: 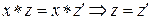 . .
Этот закон справедлив для неабелевых групп. Здесь то и различаются левое и правое деления.
Примеры групп
Рассмотрим множество всех целых чисел.При сложении двух целых чисел получается снова целое число. Если одно из слагаемых равно (целому) числу 0, то сумма равна другому слагаемому: а
+ 0 = а
; для каждого целого числа а
противоположное к нему число – а
(сумма которого с данным числом а
равна 0) тоже является целым. Операция сложения (в частности, целых) чисел коммутативна (a
+ b
= b
+ а
для любых двух чисел а
и b
)
и ассоциативна ((a
+
b
)
+ c
= a
+ (b
+ с
)для любых трех чисел а
,b
, с
).
Далее, если из множества всех целых чисел выделить подмножество чисел, делящихся на данное числоk
,
то и оно обладает такими же свойствами. Это множество тоже «замкнуто» относительно «операции сложения» — сумма любых двух чисел, делящихся на k
,
делится на k
;
это множество содержит 0 (нуль делится на любое число); и, наконец, если а
делится на k
,
то и – а
делится на k
.
Аналогичными свойствами обладают и множество всех рациональных чисел, множество всех вещественных чисел или всех комплексных чисел— каждое из них замкнуто относительно операции сложения; нуль является одновременно числом рациональным, вещественным и комплексным; для каждого (комплексного) числа а
имеется противоположное к нему число – а
такое, что а
+ (– а)
= 0, причем — а
при вещественном а
будет вещественным, а при рациональном а
— рациональным. Операция сложения в множестве комплексных чисел (а значит, и подавно, в множестве вещественных и в множестве рациональных чисел) коммутативна и ассоциативна. Все это —примеры «групп по сложению».
Рассмотрим теперь множество всех отличных от нуля вещественных чисели «операцию умножения» в нем. Произведение любых двух таких чисел — снова отличное от нуля вещественное число; произведение любого числа а
на (вещественное, отличное от нуля) число 1 равно а,
и для каждого (отличного от нуля!) вещественного числа а
имеется обратное ему (и тоже отличное от нуля) вещественное число а
–1
произведение которого на а
равно 1.
Аналогичными свойствами обладает и множество всех отличных от нуля рациональных чисел, множество всех положительных вещественных чисел или всех положительных рациональных чисел, а также множество всех отличных от нуля комплексных чисел или множество комплексных чисел, по модулюравных1. Каждое из них замкнуто относительно операции умножения, все они содержат единицу и у каждого из их элементов имеется обратный элемент, принадлежащий тому же множеству. Умножение комплексных (а значит, и вещественных, и рациональных) чисел коммутативно (ab
= b
а
для всех а
и b
)и ассоциативно ((ab
)c
= а
(b
с
)для всех а
,b
, с).
Это — примеры «групп по умножению». Можно привести и более неожиданный пример: группу по умножению образует, например, пара чисел,1 и – 1. Впрочем, множество, состоящее из одного числа1 (или 0), тоже образует группу по умножению (соответственно по сложению). Комплексные числа 1, i
,
– 1, – i
также образуют, очевидно, группу по умножению.
Складывать можно не только числа, но, например, векторылинейного пространства R
,
причем это сложение подчиняется тем же законам, что и сложение чисел: оно крммутативно и ассоциативно, в R
имеется нулевой элемент 0 такой, что х
+ 0 = х
для любого х
ÎR
,и для всякого вектора х
ÎR
имеется противоположный ему вектор – х,
такой, что х
+ (– х)
= 0.
Складывать можно матрицы одного и того же строения(т.е. [m
´n
]-матрицы, где m
и п
— какие-то заранее заданные целые положительные числа). Это сложение ассоциативно и коммутативно, имеется нулевая матрица, прибавление которой не меняет второго слагаемого — это матрица, состоящая из одних нулей, и для каждой матрицы [a
ik
]имеется противоположная к нейматрица [– a
ik
] — такая, что [a
ik
] + [– a
ik
] есть нулевая матрица. Если рассматривать только так называемые целочисленные матрицы(т.е. матрицы с целыми элементами a
ik
),то и суммой двух таких матриц будет матрица такого же строения, нулевая матрица является целочисленной, и для каждой целочисленной матрицы, противоположной к ней, будет тоже целочисленная матрица. Все это — тоже примеры групп по сложению.
С другой стороны, и перемножать можно не только числа, но, например, невырожденные квадратные матрицы одного и того же порядка п
с вещественными (или только с рациональными или, наоборот, с комплексными) элементами. Произведение двух таких матриц тоже будет невырожденной матрицей (т.к. произведение невырожденных матриц также невырожденное)
с вещественными (соответственно с рациональными, комплексными) элементами; единичная матрица является невырожденной, и у каждой невырожденной матрицы имеется обратная (тоже невырожденная и тоже с вещественными или соответственно рациональными, комплексными элементами). Умножение матриц ассоциативно, однако оно не коммутативно. Множество всех невырожденных матриц порядка п
с вещественными (рациональными, комплексными) элементами представляет собой пример некоммутативной группы по умножению.[5]
Способы задания групп
Конкретная группа может быть определена следующими способами:
1. Как множество элементов с бинарной операцией, удовлетворяющей трем групповым аксиомам. Это основное определение, из которого можно получить все другие.
2. При помощи графической схемы (сети), составленной из направленных отрезков и обладающей основными свойствами, которыми <…> должен обладать граф группы. <…>
2. При помощи квадратной таблицы символов, которую мы назвали таблицей умножения группы <…>. Такая таблица задает группу, поскольку в ней указаны все произведения элементов группы[6]
.
Хотя из таблицы умножения группы можно извлечь все то, что мы хотим знать о группе, поскольку в ней указаны все попарные произведения элементов группы, можно предвидеть ряд трудностей, которые возникнут при любой попытке неограниченно расширить область ее применения. Представьте себе, например, что вам нужно проанализировать группу порядка 60 с помощью ее таблицы умножения. <…>
Поэтому, следует рассмотреть еще одно фундаментальное понятие в теории групп, которое позволяет описывать группу способом, не зависящим от ее порядка. Речь идет об образующих элементах
группы[7]
. Это и есть еще один способ задания группы, т.е. с помощью образующих и определяющих соотношений. С основными понятиями образующих элементов познакомимся в следующем параграфе.
1.2. Образующие элементы группы. Система образующих
1.2.1. Понятие образующего элемента
Пусть а
и b
— элементы некоторой группы. Тогда, согласно аксиоме об обратных элементах, а
–1
и b
–1
также являются элементами данной группы наряду с a
b
–1
a
, abа
–1
b
и т.д. Любое произведение, которое можно записать, используя в качестве сомножителей элементы а
, b
, а
–1
, b
–1
в любом порядке и в любом конечном числе, является элементом этой группы, согласно определению бинарной операции. Если все элементы группы можно записать в виде произведений, включающих лишь а
и b
(и их обратные), то мы назовем а и b
образующими
(или образующими элементами
) группы
[8]
.
Определение
Элемент, из степеней которого составлена данная группа H
, называется образующим элементом
этой группы.
Замечание
Следует отметить, что понятию «образующий элемент» предлагают схожее по смыслу понятие «порождающий элемент» (от анг. generative — порождающий). Такое различие часто встречается в разных источниках и литературе по теории групп. И, например, вместо того, чтобы говорить: элемент а
порождает группу H
(a
), часто говорят: элемент a
есть образующий элемент
группы H
(a
).
Примеры
1. Простейший случай — это группа с одной образующей, скажем а
; все ее элементы могут быть представлены как произведения, содержащие в качестве сомножителей а
и а
–1
. Мы уже сталкивались с группой, порожденной одним элементом: группа вращений треугольника в его плоскости имеет таблицу умножения, представленную на рис. 1.2.1<…>, и так как I
= аа
–1
, то ясно, что каждый из трех элементов группы I
, а
, а2
является произведением, содержащим в качестве сомножителей лишь а
и а
–1
. [9]
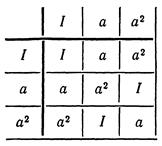
Рис. 1.2.1. Таблица умножения группы вращений треугольника
2. Знакопеременная группа An
порождается множеством 3-циклов.
3. Группа поворотов С
n
порождается одним поворотом t
= 2p/n
, а группа диэдра Dn
— поворотом t
и отражением r
относительно одной из осей.
1.2.2. Система образующих. Конечное число образующих
Однако не всякая группа имеет один образующий элемент. Есть группы, которые порождаются не одним, а с необходимостью несколькими (иногда бесконечным числом) элементами; и понятию одного образующего элемента приходит на смену понятие системы образующих
. Очевидно, совокупность всех элементов какой-нибудь группы есть (тривиальная) система образующих этой группы.
Определение 1
Некоторое множество E
элементов группы G
называется системой образующих
этой группы, если всякий элемент группы G
есть произведение конечного числа сомножителей, каждый из которых либо есть элемент множества E
, либо является обратным некоторому элементу множества E
.[10]
Или говорят, что группа G
порождается своим подмножеством E
или что E
— система порождающих (элементов) группы G
, если G
= {E
}.
Примеры
Рассмотрим плоскость с выбранной на ней системой декартовых координат. Обозначим через G
множество тех точек Р
= (х
, у
), обе координаты которых х
и у
— целые числа. Установим следующее правило сложения точек: суммой двух точек Р
1
= (x
1
, y
1
) и Р
2
= (х
2
, у
2
) называется точка Р
3
= (х
3
, у
3
) с координатами х
3
= х
1
+ х
2
и y
3
= y
1
+ y
2
. Можно легко убедится, что это определение сложения превращает множество G
в коммутативную группу и что точки (0, 1) и (1; 0) составляют систему образующих
этой группы[11]
.
Замечание
Всякая группа имеет систему образующих.
Теорема
Множество E
тогда и только тогда будет системой образующих группы G
, если всякий элемент из G может быть записан хотя бы одним способом в виде произведения числа степеней элементов из E
.
Определение 2
Если группа G
обладает системой образующих, состоящей из конечного числа элементов, то G
называется группой с конечным числом образующих.
Примеры
1. Циклическая группа — группа с одной образующей.
2. Группа  всех n
-мерных векторов с целочисленными координатами с операцией сложения имеет стандартную систему образующих e
= всех n
-мерных векторов с целочисленными координатами с операцией сложения имеет стандартную систему образующих e
=  , где , где  — вектор, у которого единственная ненулевая координата — i
-ая, равная 1. — вектор, у которого единственная ненулевая координата — i
-ая, равная 1.
3. Система {3,7} — является системой образующих группы 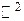 . .
Замечание 1
Всякая система образующих группы с конечным числом образующих содержит конечное подмножество, являющееся неприводимой системой образующих этой группы.
Так как конечная система образующих всегда может быть сделана неприводимой путем удаления лишних элементов, то нужно лишь доказать, что при наших предположениях всякая бесконечная система образующих содержит конечное подмножество, также являющееся системой образующих для рассматриваемой группы. Пусть G
есть группа с образующими а
1
, а
2,
…, а
n
,
G
= {а
1
, а
2,
…, а
n
},
и пусть М
есть некоторая другая система образующих этой группы. Всякий элемент а
i
, i
= 1, 2….n
, записывается в виде произведения степеней конечного числа элементов из М
. Выбирая для каждого а
i
одну из таких записей и собирая те элементы из М
, которые входят в эти записи i
= 1, 2….n
, мы получим конечное подмножество М
¢ из М
, порожденная которым подгруппа {М
¢} содержит все элементы а
1
, а
2,
..., а
n
и поэтому совпадает с G
.
Заметим, что различные неприводимые системы образующих группы с конечным числом образующих могут содержать, вообще говоря, различное число элементов. Например, в циклической группе можно выбрать неприводимые системы образующих, состоящие более чем из одного элемента. Так, систему образующих для аддитивной группы целых чисел составляют, например, числа 2 и 3.
Замечание 2
Всякая бесконечная группа с конечным числом образующих является счетной.
Действительно, если элементы а
1
, а
2,
…, а
n
являются образующими для группы G
, то всякий элемент этой группы может быть записан виде произведения
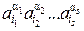
(вообще говоря, многими различными способами); всякое i
k
есть одно из чисел 1, 2,…, n
, причем возможно, что i
k
= i
l
при k
≠ l
. Будем называть длиной этого произведения сумму абсолютных величин показателей:
h
= |α1
| + |α2
| + … + |αs
|.
Легко видеть, что существует лишь конечное число произведений степеней образующих элементов а
1
, а
2,
…, а
n
данной длины h
. Множество всех произведений степеней этих элементов будет, следовательно, суммой счетного множества, т.е. счетным, а поэтому и группа G
будет не более чем счетной[12]
.
Существуют счетные группы, не имеющие конечных систем образующих. Примером таких групп являются числа  , составляющие систему образующих для аддитивной группы рациональных чисел R
. , составляющие систему образующих для аддитивной группы рациональных чисел R
.
Группы с конечным числом образующих составляют, следовательно, класс групп, промежуточный между конечными и счетными группами.
Примеры
1. Примером группы с двумя образующими служит таблица умножения группы самосовмещений равностороннего треугольника.
2. Знакопеременная группа А
n
порождается множеством 3-циклов.
3. Группа поворотов С
n
порождается одним поворотом t
= 2p/n
. А группа диаэдра D
n
— поворотом t
и отражением r
относительно одной из осей.[13]
Два важных примера систем образующих содержатся в приводимых ниже теоремах.
Подстановка, являющаяся циклом длины 2, называется транспозицией[14]
.
Теорема
1
Группа S
n
порождается транспозициями.
Доказательство
Отметим, что каждая транспозиция обратна сама себе. Поэтому утверждение теоремы означает, что любая подстановка разлагается в произведение транспозиций.
Умножение подстановки
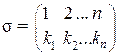 . .
слева на транспозицию (
ij
)
вызывает перестановку i
и j
в нижней строке. Такая операция также называется транспозицией. Очевидно, что путем последовательных транспозиций любую перестановку (k
1
, k
2
, …, kп
)можно привести к тривиальной: сначала, если k
1
¹ 1, меняем местами k
1
и 1, ставя тем самым 1 на первое место, затем ставим 2 на второе место и т.д. Таким образом, существуют такие транспозиции t
1
, t
2
,…,
t
n
что
t
n
…t
2
t
1
s= id
,
и, значит,
s =
t
1
t
2
…
t
n
.
Теорема
2
Группа QL
n
(K
) порождается элементарными матрицами[15]
.
Доказательство
Отметим, что матрица, обратная к элементарной, также элементарна. Поэтому утверждение теоремы означает, что любая невырожденная матрица разлагается в произведение элементарных матриц.
Умножение матрицы А
Î
GL
n
(
K
)
слева на элементарную матрицу вызывает соответствующее элементарное преобразование ее строк. Мы знаем, что с помощью элементарных преобразований строк любую невырожденную матрицу можно привести к единичной матрице. Таким образом, существуют такие элементарные матрицы U1
,U2
,..., U
s
,что
U
s
…
U2
U1
A
= Е
,
и, значит,
A
=
U1
–1
U2
–1
…U
S
–1
.[16]
1.2.3. Непорождающие элементы
Антиподом порождающих множеств является подгруппа Фраттини. Чтобы прийти к этому понятию, назовем подгруппу Н
группы G
максимальной подгруппой со свойством s, если Н
обладает свойством s и не содержится ни в какой большей подгруппе с этим свойством. Если s — свойство быть меньше всей группы, то максимальные подгруппы со свойством s называются просто максимальными. Конечно, в группе может и не быть максимальных подгрупп <…>. По определению подгруппа Фраттини
Ф
(G
) группы G
— это пересечение всех ее максимальных подгрупп, если они существуют, и сама G
— в противном случае.
Элемент х
группы G
назовем непорождающим элементом
группы, если его можно удалить из любого порождающего множества группы G
, в которое он входит.
Теорема
Множество S
всех непорождающих элементов группы G
совпадает с подгруппой Фраттини Ф
(G
).
Доказательство
а) S
ÍФ
(G
). Действительно, если G
не содержит максимальных подгрупп, то утверждение тривиально. Пусть теперь х
ÎS
, Н
— максимальная подгруппа из G
*. Если х
ÏН
, то (х
, Н
) = G
, (Н
) ÏG
. Это противоречит включению х
ÎS
. Значит, х
ÎН
, х ÎФ
(G
).
б) Ф
(G) ÍS
. Пусть, напротив, существует элемент х
ÎФ
(G
), который вместе с некоторым множеством М
порождает G
, но (М
) ¹G
. По лемме Цорна существуют подгруппы Н
, максимальные среди подгрупп, содержащих М
и не содержащих х
. Ясно, что все эти подгруппы просто максимальны. Но тогда они содержат Ф
(G
), а вместе с ней х
, вопреки построению. Теорема доказана[17]
.
Примеры
1. В группе  подгруппа (р
) максимальна при любом простом р
, поэтому Ф
( подгруппа (р
) максимальна при любом простом р
, поэтому Ф
( ) = 0. Легко сообразить, что в группе ) = 0. Легко сообразить, что в группе  любой элемент является непорождающим, поэтому Ф
( любой элемент является непорождающим, поэтому Ф
( ) = ) =  . .
2. Так как группа Ср
∞
совпадает с объединением подгрупп Ср
n
, n
=1, 2,…, то каждый ее элемент является непорождающим. Поэтому Ф
(Ср
∞
) = Ср
∞
.
3. Можно проверить, что подгруппа H
i
группы S
n
, состоящая из всех подстановок, оставляющих символ i
неподвижным, максимальна в S
n
. Так как пересечение H
1
Ç…ÇH
n
равно 1, то Ф
(S
n
) = 1.
1.3. Циклические группы
1.3.1. Подгруппа, порожденная данным элементом данной группы. Определение циклической группы
Пусть а
— произвольный элемент группы G
. Умножим его на себя, т.е. возьмем элемент а
∙а
. Этот элемент обозначим через а
2
. Точно так же обозначим а
∙а
∙а
через а
3
и вообще положим а
∙а
∙…∙а
= а
n
.
Рассмотрим далее, элемент а
–1
и обозначим последовательно
а
–1∙
а
–1
через а
–2
а
–1∙
а
–1∙
а
–1
через а
–3
а
–1∙
а
–1
∙…∙ а
–1
через а
–
n
.
Обозначения эти оправданы тем, что, действительно,
а
n
∙а
–
n
= 1.
Для доказательства последнего утверждения заметим прежде всего, что в случае п
= 1 оно очевидно (следует из самого определения а
–1
). Предположим, что оно верно для п
–1 и докажем в этом предположении его справедливость для п
. Имеем
а
n
∙а
–
n
= (а
n
∙ а
n–1
) (а
–(
n–1)
∙а
–1
) = а
∙{а
n–1
∙а
–(
n–1)
}∙а
–1
.
Но в силу нашего предположения фигурная скобка равна единице, значит,
а
n
∙а
–
n
= а
∙1∙ а
–1
= 1.
что и требовалось доказать.
Мы определили выражение а
n
для любого положительного и для любого отрицательного значения п
. Положим, наконец, что, по определению, а
0
= 1.
Пусть теперь р
и q
— два целых числа. Из наших определений следует, что для любых целых р
и q
имеем
ар
∙а
q
= ар
+q
.
Мы получаем следующий результат.
Множество Н
(а
) тех элементов группы G
, которые могут быть представлены в виде ап
при целом п
с той групповой операцией, которая задана в группе G
, образует группу Н
(а
).
В самом деле: 1) произведение двух элементов, принадлежащих Н
(а
), есть опять элемент Н
(а
); 2) единица принадлежит Н
(а
); 3) к каждому элементу аm
из Н
(а
) найдется элемент а–
m
, который также принадлежит Н
(а
).
Итак, Н
(а
) есть подгруппа G
. Эта подгруппа называется циклической подгруппой группы G
, порожденной элементом а
.
[18]
Определение
Если любой элемент группы выражается в виде степени единственной образующей, то группа называется циклической
.
Примеры
1. Примером циклической группы может служить группа вращений правильного многоугольника. Пусть дан правильный n
-угольник A
1
A2
...
A
n
,и пусть О
— его центр. Рассмотрим всевозможные повороты плоскости вокруг точки О,
при которых этот n
-угольник совмещается сам с собой. Таких поворотов, очевидно, п
:
a
0
—поворот на Ð 0 (тождественное преобразование),
a
1
— поворот на 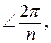
a
2
— поворот на 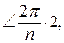
…………………
a
n
–1
— поворот на 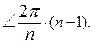 . .
По определению, умножение
поворотов — это их последовательное выполнение одного за другим:
a
k
◦ a
i
= a
k+I
,
при этом естественно считать, что a
k+
n
= a
k
для любого k
, в частности, а
п
= а
0
.
Это умножение, очевидно, ассоциативна (и коммутативно). Поворот а
0
является единичным элементов группы и a
k
–1
= а
п —
k
.
для всех k
= 0, 1, ...., n
– 1.
Если положить а
1
= а
,мы будем иметь а
2
= а
2
, а
3
= a
3
, a
n
–1
= а
n–
1
и, наконец, а
п
= а
п
= а
0
.
Можно сказать, что эта группа образована степенями одного из своих элементов(или что она «порождается»
одним из своих элементов), а именно, элемента а
= а
1
.
Группа вращений правильного n
-угольника является циклической группой порядка
п
;обозначается эта группа символом С
п
.
2. Циклической группой порядка 3 является группа вращений треугольника. Выписав степени образующей а
:
а
, а
2
, а
3
, а
4
, а
5
, а
6
, а
7
,… .
Так как а
3
= I
, то эту последовательность можно переписать так:
а
, а
2
, I
, а
, а
2
, I
, а
,… .
Она представляет собой циклическое повторение основной серии а
, а
2
, I
. Именно по этой причине данная группа — циклическая.
3. Группа целых чисел (по сложению) тоже является циклической — она порождается одним из своих элементов: ведь 2 = 1 + 1, 3 = (1 + 1)+ 1, — 1 есть элемент, противоположный к 1, и т.д. Эта группа является бесконечной циклической группой
; обозначается она символомС
∞
[19]
.
Замечание
Обычно мы будем использовать для обозначения циклической группы букву С
, а ее порядок обозначать числом в нижнем индексе. Таким образом, С
3
обозначает циклическую группу порядка 3, а С
n
— циклическую группу порядка n
.[20]
Таким образом, мы определили понятие циклической подгруппы Н
(а
), порожденной некоторым элементом а
данной группы G
.
Замечание
Всякая циклическая группа, коммутативна.
Доказательство
Поскольку в группе Н
(а
)
ар
∙а
q
= ар
+
q
= а
q
+
p
= а
q
∙а
р
.
то группа Н
(а
) коммутативна.[21]
Бесконечная циклическая группа
Циклическая группа определяется тем свойством, что все ее элементы можно выразить как степени одного образующего элемента а
. Выяснили, что группа, порожденная элементом а
, конечна, если существует положительное число n
, такое, что а
n
= I
. Если же такого положительного целого числа не существует, то каждая следующая степень элемента а
представляет собой новый элемент группы, и в таком случае циклическая группа будет бесконечной
.
Примеры
1. Конечной циклической группой порядка n
является мультипликативная группа корня n
-ой степени из единицы, n
= 1, 2, …
2. Бесконечной циклической группой является аддитивная группа целых чисел, ее образующим элементом является число 1.
Пример бесконечной циклической группы показывает, что из конечности числа образующих не следует конечность самой группы.
Теорема
В циклической группе G
= {а
} порядка n
в качестве образующего элемента можно взять элемент a
k
, 0 ≤ k
< n
, тогда и только тогда, если k
и n
взаимно просты.
Доказательство
Действительно, если (k
, n
) = 1, то существует такие u
и v
, что
ku
+ nv
= 1.
Тогда
(а
k
)u
= а
1 –
nv
= а
∙ а
–
nv
= а
.
Если, с другой стороны, при некотором k
будет (а
k
)s
= а
, то разность показателей ks
– 1 должна делится на n
.
ks
– 1 = nq
,
откуда ks
– nq
= 1, т.е. (k
,n
) = 1. Что и требовалось доказать.[22]
ГЛАВА 2. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ГРУПП
Одними из ключевых вопросов теории групп являются вопросы задания и построения конкретной группы или некоторого их класса. В предыдущей главе были приведены способы задания различных групп. Пожалуй, самым интересным и довольно наглядным способом задания групп является так называемое графическое представление, т.е. с помощью графов. А понятие образующей группы играет здесь основную роль при переходе к осуществлению графического представления групп. Остановимся подробней на данном вопросе.
Если элемент а
порождает циклическую группу С
n
, то последовательность степеней элемента а
представляет собой циклическое повторение основной серии а
, а
2
, ..., а
n
= I
. Это свойство допускает геометрическую интерпретацию, которая в свою очередь приводит к осуществлению нашей цели — построению графического представления группы. Например, циклическая группа порядка 3 (из примера главы 1 о циклических группах) наводит на мысль о треугольнике, каждая вершина которого соответствует элементу группы (рис. 2.1).
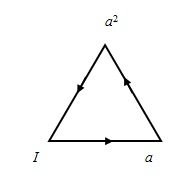
Рис.2.1
Каждой стороне треугольника приписано направление, которое указано стрелкой. Движение в направлении, указанном стрелкой, соответствует умножению справа на образующий элемент а
группы. Таким образом, отправляясь из вершины, помеченной символом а
2
, передвинуться в направлении, указанном стрелкой, к вершине I
— это все равно, что образовать произведение а
2
а
= а
3
= I
. Движение в направлении, противоположном указанному стрелкой, соответствует умножению справа на элемент а
–1
, обратный к образующей а
. Например, отправляясь из вершины, помеченной символом а
2
, передвинуться в направлении, противоположном указанному стрелкой, направленной к этой вершине, — это все равно, что образовать произведение а
2
а
–1
= a
a
а
–1
= a
.
2.1. Граф группы
Возникает предположение, что многоугольник, сторонам которого приписано направление, можно рассматривать как геометрический эквивалент циклической группы, или граф
циклической группы. Давайте посмотрим, что мы знаем об основных свойствах группы и как они отражаются в только что предложенной геометрической интерпретации.
Если а
— образующая циклической группы, то по определению каждый элемент может быть представлен как произведение сомножителей а
и а
–1
. Обратно, любое произведение сомножителей а
и а
–1
есть элемент группы. Рассмотрим, например, произведения
а,
аа а
–1
, а
–1
аа а
–1
а
ясно, что все три произведения представляют собой один и тот же элемент группы.
По очевидной аналогии мы назовем конечную последовательность образующих и их обратных словом
. Тогда каждому слову, составленному из символов а
и а
–1
(как мы будем говорить, «слову от символов а
и а
–1
»), соответствует элемент циклической группы, порожденной а
. Так как любой наперед заданный элемент может быть представлен в виде слова бесконечно многими способами, то представление элемента группы в виде слова неоднозначно.
Если х
— некоторый элемент циклической группы порядка 3, то любое слово, представляющее элемент х
, можно понимать как движение по графу<…>. Пусть слово ааа
–1
представляет элемент х
. Будем интерпретировать его как такое движение по графу, изображенному на рис. 2.1.1:
1. Возьмем за исходную точку вершину, помеченную символом I
. Так как первым сомножителем в слове, представляющем элемент х
, является а
, мы движемся из I
в направлении, указанном стрелкой
, к другому концу отрезка, который изображен на рис. 2.1.2. Этот конец является вершиной, помеченной символом а
, и будет служить исходной точкой для дальнейшего движения.
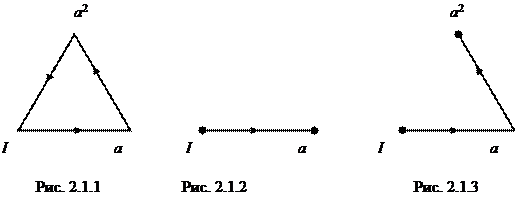
2. Так как второй сомножитель равен а
, мы выходим из достигнутой на первом шаге вершины и движемся в направлении, указанном стрелкой
, к другому концу отрезка (рис. 2.1.3). Этот конец есть вершина, помеченная символом а
2
; он и будет служить исходной точкой для дальнейшего Движения.
3. Так как третий сомножитель есть а
–1
, обратный к а
, мы отправляемся из вершины, в которую пришли на втором шаге, и движемся в направлении, противоположном указанному стрелкой, к другому концу отрезка. Этот конец — вершина, помеченная символом а
, — мог бы служить исходной точкой для дальнейшего движения. Однако в данном слове третий сомножитель последний, и потому дальнейших движений не происходит, т.е. путь, соответствующий слову ааа
–1
заканчивается в вершине, помеченной символом а
.
Слово, соответствующее элементу х
, интерпретируется, таким образом, как множество направлений при движении вдоль некоторого пути в графической сети. Каждому слову соответствует определенная последовательность движений вдоль направленных отрезков, и, обратно, любой путь вдоль направленных отрезков графа группы, начинающийся из вершины I
, соответствует конкретному слову.
Представление группы как сети, состоящей из направленных отрезков (или ребер), где вершины соответствуют элементам, а отрезки — умножению на образующие группы и их обратные, было введено Кэли еще в XIX веке. Такая сеть, или граф, часто называется диаграммой Кэли
.
Вращения квадрата в его плоскости <…> составляют циклическую группу порядка 4, С
4
. Граф этой группы представлен на рис. 2.1.4.

Замечания
1) Вершин у графа столько же, сколько элементов в группе.
2) Вершина I
выбирается произвольно.
3) В каждой вершине сходятся два отрезка, один соответствует умножению справа на образующую а
и направлен от вершины, а другой соответствует умножению справа на элемент а
–1
, обратный к образующей, и направлен к вершине.
4) Конкретная форма графической сети не имеет значения. Важна лишь конфигурация связей между вершинами. Направленные отрезки, связывающее вершины, не обязаны быть прямолинейными, а граф не обязан иметь форму правильного многоугольника. Вы можете проявить свой вкус, выбирая ту форму, которая вам нравится, если только при этом не искажается математический смысл.
Графом циклической группы С
n
порядка n
, связанной с вращениями правильного n
-угольника в его плоскости, является n
-угольник с направленными отрезками в качестве сторон. Например, циклическая группа порядка 6, С
6
, соответствующая самосовмещениям правильного шести-угольника, вращающегося в своей плоскости, состоит из элементов а
, а
2
, а
3
, а
4
, а
5
и a
6
= I
. Шестиугольник, ребрами которого являются отрезки, направленные как на рис. 2.1.5, будет графом этой группы.

2.1.1.
Бесконечная циклическая группа
Теперь мы построим граф бесконечной
циклической группы. Циклическая группа определялась тем свойством, что все ее элементы можно выразить как степени одного образующего элемента а
. Группа, порожденная элементом а
, конечна, если существует положительное целое число n
, такое, что а
n
= I
. Если такого положительного целого числа не существует, то каждая следующая степень элемента а
представляет собой новый элемент группы, и в таком случае циклическая группа будет бесконечной
. Бесконечная аддитивная группа <…>представляет собой пример такой группы.
Конечную циклическую группу можно связать с самосовмещениями правильного n
-угольника на плоскости и прийти к соответствующей диаграмме Кэли. Чтобы построить граф бесконечной циклической группы, нам также будет удобно опираться на некоторое геометрическое представление. Рассмотрим прямую линию, разделенную на равные интервалы, скажем, длины 1, и ее самосовмещения, которые сдвигают эту линию вдоль самой себя на одну или несколько единиц вправо или влево. Множество всех таких самосовмещений есть бесконечная циклическая группа, порожденная сдвигом на единицу вправо. Диаграмма Кэли этой группы представлена на рис. 2.1.6.
Примечания
1) Естественным образом обобщив наши предыдущие обозначения, мы обозначим бесконечную циклическую группу через С
¥
.
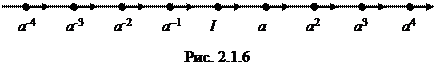
2) Ясно, что за I
можно взять любую вершину.
3) Снова мы видим, что в каждой вершине сходятся два направленных отрезка. Движение от вершины вдоль отрезка в направлении, указанном стрелкой, соответствует умножению справа на образующую а
; движение в направлении, противоположном указанному стрелкой, соответствует умножению справа на а
–1
.<…>
2.1.2.
Группа с двумя образующими
Таблица умножения группы самосовмещений равностороннего треугольника является примером группы с двумя образующими: вращением r
и опрокидыванием f
. Элементами этой группы <…> являются
I
,
r
,
r
2
f
,
fr
,
fr
2
,
где каждый элемент первой строки получается из соседнего слева (справа) умножением справа на r
(или r
–1
), а элементы второй строки получаются из элементов первой умножением слева на f
. Это наводит на мысль, что для графа этой группы надо использовать два треугольника, соединенные отрезками, соответствующими образующей f
(рис. 2.1.7).

Мы отличаем на графе образующую r
от образующей f
, используя непрерывную линию для умножения на r
и пунктирную для умножения на f
. Сам Кэли предлагал различные образующие выделять различными цветами и называл этот процесс графического представления методом цветных групп.
В качестве следствия того факта, что рассматриваемая группа имеет две образующие, мы получаем, что любой путь нашего графа может быть описан последовательностью, содержащей лишь символы из множества
r, f, r
–1
, f
–1
.
Примерами таких последовательностей являются
rfr
–1
f
–1
иrf
–1
rf
–1
r
1
,
которые мы, как и раньше, будем называть словами
. Конечно, каждое слово от образующих и их обратных является элементом группы или, говоря точнее, представляет элемент группы.
Произведение любых двух элементов, определенное с помощью таблицы умножения этой группы <…>, совпадает с произведением, полученным с помощью графа, изображенного на рис. 6.7. Чтобы, например, проверить равенство rf
= fr
2
, пройдем сначала r
-отрезок, выходящий из I
, а затем f
-отрезок, входящий в вершину, помеченную символом fr
2
(рис. 2.1.8). Путь на рис. 2.1.9 показывает, что frrf
= r
.
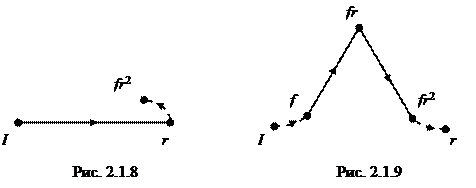
2.2. Основные свойства графа группы
Наши примеры графов различных групп имеют некоторые общие существенные свойства.
Элементы группы находятся во взаимно однозначном соответствии с вершинами графа
. Каждая вершина графа соответствует в точности одному элементу группы, и наоборот.
Каждое ребро графической сети есть направленный отрезок, и отрезки одного «цвета» связаны с одной и той же образующей группы
. Движение, начинающееся в некоторой вершине, вдоль отрезка в направлении, указанном стрелкой, соответствует умножению справа на связанный с этим отрезком образующий элемент (назовем его а
), в то время как движение вдоль отрезка в направлении, противоположном указанному стрелкой, соответствует умножению справа на а
–1
— элемент, обратный к образующей. Например, если А
, В
и С
на рис. 2.2.1 суть вершины графа, соответствующие элементам х
, y
и z
некоторой группы соответственно, то движение от В
к С
отвечает умножению элемента у
на а
, так что уа
–1
= z
, а движение от В
к A
отвечает умножению элемента у
на а
–1
, т.е. у а
–1
= х
.
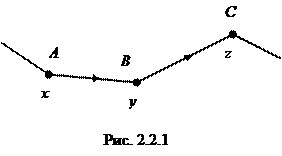

Каждое слово, представляющее элемент группы, можно интерпретировать как путь, или некоторую последовательность направленных отрезков графа, и наоборот
. В каждой вершине пути, соответствующего некоторому слову, очередное движение определяется следующим сомножителем в слове. Так как любой сомножитель — это или одна из образующих, или элемент, обратный к образующей, то каждая вершина является концевой точкой двух направленных отрезков одинакового «цвета» — одного, направленного к вершине, и другого, направленного от нее. Если группа имеет две образующие, а
и b
, то в каждой вершине сходятся четыре ребра, так как четыре элемента a
, a
–1
, b
, b
–l
соответствуют четырем возможным движениям, начинающимся в этой вершине. Вообще в каждой вершине есть одно «входящее» и одно «исходящее» ребро для каждой образующей.
Умножение двух элементов группы соответствует прохождению на графе пути, составленного из двух последовательных путей
.
Произведение rs
= t
элементов r
и s
группы можно интерпретировать как путь в графе, который строится следующим образом. Запишем r
и s
как слова от образующих и их обратных. Выходя из вершины, соответствующей элементу I
, пройдем путь, описанный словом, определенным элементом r
. Конечная точка этого пути соответствует элементу r
. Теперь, принимая за начальную точку r
-вершину[23]
(т.е. вершину, соответствующую элементу r
), пройдем путь, описанный словом, соответствующим элементу s
. Этот путь закончится в вершине, соответствующей элементу t
= rs
, вне зависимости от того, какие слова используются для представления элементовr
и s
.

Любое слово, представляющее элемент I
, соответствует замкнутому пути на графе.
Предположим, что W
— слово, представляющее элемент I
. Например, в группе самосовмещений равностороннего треугольника за W
можно взять frfr
. Если принять вершину, соответствующую элементу I
, за начальную точку, то путь, определяемый словом W
, окончится в I
-вершине. Мы называем путь замкнутым
, если его начальная и конечная точки совпадают. Если за начальную точку взята вершина, соответствующая элементу t
, отличному от I
, то путь, заданный словом W
, окончится в t
-вершине, так как tW
— t. Таким образом, если W
— слово, представляющее элемент I
, то путь, определяемый этим словом, будет замкнутым вне зависимости от того, какая точка принята за начальную.
Таким образом, граф группы обладает некоторым свойством однородности.[24]
(Произвольный граф называется однородным
степени n
если в каждую его вершину входит и из каждой его вершины выходит одинаковое число направленных отрезков, равное n
. Граф группы будет однородным графом в этом смысле). Из этого свойства графа группы следует, что его вершины можно пометить так, чтобы любая наперед заданная вершина соответствовала элементу I
.<…>
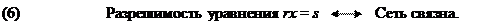
Граф группы является связной сетью, т.е. существует путь из любой вершины в любую другую вершину
. Если r
и s
— два произвольных элемента группы, то существует элемент х
= r
–l
s
, такой, что rx
= s
<…>. Ясно, что если W
— произвольное слово, представляющее элемент х
= r
–1
s
, то rW
= s
; таким образом, если вершина, соответствующая элементу r
, взята за начальную точку, то путь, описанный словом W
, ведет от r
-вершины к s
-вершине.
Теперь выпишем вместе все соответствия, установленные в ходе предыдущих рассуждений:
| Группа |
Граф |
| Элемент |
Вершина |
| Образующая |
Направленные ребра одного «цвета» |
| Слово |
Путь |
| Умножение элементов |
Последовательное прохождение путей |
| Слово, представляющее элемент I
|
Замкнутый путь |
| Разрешимость уравнения rx
= s
|
Сеть связна |
Таким образом, конкретная группа может быть определена при помощи графической схемы (сети), составленной из направленных отрезков и обладающей основными свойствами, которыми (как мы установили) должен обладать граф группы. Внутренней структурой такой сети группа вполне определяется, т.к. нам известно, каким образом последовательному прохождению путей должно соответствовать умножение элементов группы.[25]
А из приведенных выше соответствий видно, что образующая в группе соответствует направленным ребрам одного «цвета» в графе, а каждый элемент группы соответствует вершинам в графе.
ЛИТЕРАТУРА
1. Введение в теорию групп / П. С. Александров — М.: Издательство «Наука», 1980. — С. 144.
2. Группы и их графы / И. Гроссман, В. Магнус; под ред. В. Е. Тараканова — М.: Издательство «Мир», 1971. — С. 245.
3. Курс алгебры / Э. Б. Винберг— 2-е изд., испр. и доп. М.: Изд-во «Факториал Пресс», 2001— С. 544.
4. Лекции по математике. Т. 8 / Теория групп: учебн. пособие / В. Босс — М.: КомКнига, 2007. — С. 216.
5. Линейная алгебра и некоторые приложения / Л. И. Головина. — 3-е изд., перераб. и доп. — М.: Издательство «Наука», 1979. — С. 392.
6. Основы теории групп / М. И. Каргаполов, Ю. И. Мерзляков. — 3-е изд., перераб. и доп.— М.: Наука, 1982.— С. 288.
7. Теория групп / А. Г. Курош. — М.: Издательство «Наука», 1967. — С. 648.
8. Группа (математика) // Википедия / Свободная энциклопедия [Электронный ресурс]. ¾ Режим доступа: http://ru.wikipedia.org
[1]
Множество М
с одной бинарной алгебраической операцией принято теперь называть группоидом
.
[2]
Теория групп / А. Г. Курош. — М.: Издательство «Наука», 1967. — С. 16–17.
[3]
Линейная алгебра и некоторые приложения / Л. И. Головина. — 3-е изд., перераб. и доп. — М.: Издательство «Наука», 1979. — С. 274–276.
[4]
Группа (математика) // Википедия / Свободная энциклопедия [Электронный ресурс]. ¾ Режим доступа: http://ru.wikipedia.org
[5]
Линейная алгебра и некоторые приложения / Л. И. Головина. — 3-е изд., перераб. и доп. — М.: Издательство «Наука», 1979. — С. 272–275.
[6]
Группы и их графы / И. Гроссман, В. Магнус; под ред. В. Е. Тараканова — М.: Издательство «Мир», 1971. — С. 78.
[7]
Группы и их графы / И. Гроссман, В. Магнус; под ред. В. Е. Тараканова — М.: Издательство «Мир», 1971. — С. 78.
[8]
Тот же
[9]
Группы и их графы / И. Гроссман, В. Магнус; под ред. В. Е. Тараканова — М.: Издательство «Мир», 1971. — С. 59–61.
[10]
Введение в теорию групп / П. С. Александров — М.: Издательство «Наука», 1980. — С. 61.
[11]
Введение в теорию групп / П. С. Александров — М.: Издательство «Наука», 1980. — С. 62.
[12]
Теория групп / А. Г. Курош. — М.: Издательство «Наука», 1967. — С. 43–44.
[13]
Лекции по математике. Т. 8 / Теория групп: учебн. пособие / В. Босс — М.: КомКнига, 2007. — С. 107.
[14]
Транспозиция — операция перемещения двух элементов перестановки.
[15]
Элементарной матрицей называется матрица, полученная из единичной матрицы в результате одного из следующих элементарных преобразований:
Умножение строки (столбца) матрицы на скаляр 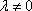
Прибавление к какой либо строке (столбцу) матрицы другой строки (столбца), умноженный на скаляр 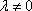 . Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица. . Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
[16]
Курс алгебры / Э. Б. Винберг— 2-е изд., испр. и доп. М.: Изд-во «Факториал Пресс», 2001— С. 164–166.
[17]
Основы теории групп / М. И. Каргаполов, Ю. И. Мерзляков. — 3-е изд., перераб. и доп.— М.: Наука, 1982.— С. 27–28.
[18]
Введение в теорию групп / П. С. Александров — М.: Издательство «Наука», 1980. — С. 55–56.
[19]
Линейная алгебра и некоторые приложения / Л. И. Головина. — 3-е изд., перераб. и доп. — М.: Издательство «Наука», 1979. — С. 276.
[20]
Группы и их графы / И. Гроссман, В. Магнус; под ред. В. Е. Тараканова — М.: Издательство «Мир», 1971. — С. 59–60.
[21]
Тот же.
[22]
Теория групп / А. Г. Курош. — М.: Издательство «Наука», 1967. — С. 41.
[23]
То есть вершину, соответствующую элементу r
.
[24]
Произвольный граф называется однородным степени n
, если в каждую его вершину входит и из каждой вершины выходит одинаковое число направленных отрезков, равное n
. Граф группы будет однородным в этом смысле.
[25]
Группы и их графы / И. Гроссман, В. Магнус; под ред. В. Е. Тараканова — М.: Издательство «Мир», 1971. — С. 62–77.
|