ÐÅÖÅÍÇÈß
íà äèïëîìíóþ ðàáîòó ñòóäåíòà V êóðñà
ôèçèêî-ìàòåìàòè÷åñêîãî ôàêóëüòåòà ÀÃÏÈ
Áîëüøàêîâà À. À. íà òåìó:
“Òðè êðèçèñà â ðàçâèòèè ìàòåìàòèêè”
Ðàçâèòèå ìàòåìàòèêè íå îäíàæäû ïðèâîäèëî â ïðîøëîì ê íåîáõîäèìîñòè îñìûñëåíèÿ è ïåðåñòðîéêè å¸ îñíîâ. Äèïëîìíàÿ ðàáîòà Áîëüøàêîâà À. À. ïîñâÿùåíà îáçîðó òðåõ ïåðèîäîâ èíòåíñèâíûõ ïîèñêîâ ïóòåé ïðåîäîëåíèÿ íàêîïèâøèõñÿ âíóòðåííèõ ïðîòèâîðå÷èé: àíòè÷íûé ïåðèîä, ïåðèîä îáîñíîâàíèÿ àíàëèçà è òåîðåòèêî-ìíîæåñòâåííûé ïåðèîä.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
 ðàáîòå ïðèâîäèòñÿ ìíîãî èíòåðåñíûõ èñòîðè÷åñêèõ ñâåäåíèé. Ïîêàçàíû íåïðîñòûå ïóòè ôîðìèðîâàíèÿ íåêîòîðûõ îñíîâíûõ ìàòåìàòè÷åñêèõ ïîíÿòèé.
Àâòîð ïîêàçûâàåò ãëóáîêîå ïðîíèêíîâåíèå â òåìó è õîðîøåå âëàäåíèå ìàòåðèàëîì. Äèïëîìíàÿ ðàáîòà Áîëüøàêîâà À. À. çàñëóæèâàåò âûñîêîé îöåíêè.
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
Çàâåäóþùèé êàôåäðîé
ìàòåìàòè÷åñêîãî àíàëèçà,
êàíäèäàò ôèçèêî-ìàòåìàòè÷åñêèõ
íàóê
Çàõàðîâ Ñ. À.
Ìèíèñòåðñòâî îáðàçîâàíèÿ Ðîññèéñêîé Ôåäåðàöèè
Àñòðàõàíñêèé ïåäàãîãè÷åñêèé èíñòèòóò èì. Ñ. Ì. Êèðîâà
Òðè êðèçèñà
â ðàçâèòèè ìàòåìàòèêè
ÄÈÏËÎÌÍÀß ÐÀÁÎÒÀ
студента физико-математического
факультета
Научный руководитель
Ованесов Н. Г.
Àñòðàõàíü · 96
Îãëàâëåíèå
Ââåäåíèå
I. Ñïîñîáû îáîñíîâàíèÿ ìàòåìàòèêè â äðåâíåé Ãðåöèè îò Ïèôàãîðà äî Åâêëèäà.
1. Ìàòåìàòèêà ïèôàãîðåéöåâ
2. Ïðîáëåìà áåñêîíå÷íîñòè â äðåâíåãðå÷åñêîé ôèëîñîôèè è ìàòåìàòèêå
3. Òðè çíàìåíèòûõ çàäà÷è äðåâíîñòè
4. Ïðåîäîëåíèå êðèçèñà îñíîâ äðåâíåãðå÷åñêîé ìàòåìàòèêè
II. Ñïîñîáû îáîñíîâàíèÿ ìàòåìàòèêè â XVIII è â ïåðâîé ïîëîâèíå XIX âåêà
1. Îñîáåííîñòè ñïîñîáîâ îáîñíîâàíèÿ ìàòåìàòèêè â êîíöå XVII è â XVIII âåêå
2. Ðàçðàáîòêà ñïîñîáîâ îáîñíîâàíèÿ ìàòåìàòèêè â ïîñëåäíåé ÷åòâåðòè XVIII è ïåðâîé ïîëîâèíå XIX âåêà
III. Ñïîñîáû îáîñíîâàíèÿ ìàòåìàòèêè â ïîñëåäíåé ÷åòâåðòè XIX âåêà è íà÷àëà XX âåêà
1. Òåîðèÿ ìíîæåñòâ. Îñíîâíûå ïîíÿòèÿ ó÷åíèÿ î ìíîæåñòâàõ Ã. Êàíòîðà
2. Òðóäíîñòè ïîñòðîåíèÿ òåîðèè ìíîæåñòâ. Êðèòèêà êîíöåïöèè Ã. Êàíòîðà
3. Ïàðàäîêñû (àíòèíîìèè) òåîðèè ìíîæåñòâ
4. Àêñèîìàòè÷åñêèå ïîñòðîåíèÿ òåîðèè ìíîæåñòâ ïî Öåðìåëî
5. Ïðîáëåìà ñóùåñòâîâàíèÿ â ìàòåìàòèêå
Ñïèñîê ëèòåðàòóðû.
Ñîçäàíèå íîâûõ è äàëüíåéøåå ðàçâèòèå ñóùåñòâóþùèõ ìàòåìàòè÷åñêèõ òåîðèé ñâÿçàíî îáû÷íî ñ óòî÷íåíèåì (îáîáùåíèåì) èõ èñõîäíûõ îñíîâíûõ ïîíÿòèé è ïîñûëîê è îñíîâàííûõ íà íèõ ìåòîäîâ. Ìàòåìàòèêè íåðåäêî âñòðå÷àëèñü ñ òðóäíîñòÿìè, ïðåîäîëåòü êîòîðûå èì óäàâàëîñü òîëüêî ïîñëå ïðîäîëæèòåëüíûõ ïîèñêîâ. Ýòè òðóäíîñòè ðîñòà ìàòåìàòèêè — òðóäíîñòè å¸ îáîñíîâàíèÿ: îíè áûëè, åñòü è áóäóò â äàëüíåéøåì.
Òðóäíîñòè îáîñíîâàíèÿ ìàòåìàòèêè èãðàþò íàèáîëåå çíà÷èòåëüíóþ ðîëü â ðàçâèòèè ìàòåìàòèêè òîãäà, êîãäà âîçíèêàåò íåîáõîäèìîñòü â êîðåííîé ïåðåðàáîòêå îñíîâ è ìåòîäîëîãèè âñåõ (èëè äîñòàòî÷íî áîëüøîãî ÷èñëà) ìàòåìàòè÷åñêèõ òåîðèé.  ýòèõ ñëó÷àÿõ ãîâîðÿò î êðèçèñå îñíîâ ìàòåìàòèêè. Èçâåñòíû òðè òàêèõ êðèçèñà.
Âïåðâûå êðèçèñ îñíîâ íàóê âîçíèê â ìàòåìàòèêå â äðåâíåé Ãðåöèè, â íà÷àëå å¸ ôîðìèðîâàíèÿ êàê íàó÷íîé ñèñòåìû. Âòîðîé èìåë ìåñòî â êîíöå XVII è â XVIII âåêå. Òðåòèé âîçíèê â êîíöå XIX âåêà, îí íå ïðåîäîëåí è â íàøå âðåìÿ è îêàçûâàåò âëèÿíèå íà ðàçâèòèå ñîâðåìåííîé ìàòåìàòèêè.
Ìû ðàññìîòðèì ñóùíîñòü ýòèõ êðèçèñîâ ìàòåìàòèêè, èìåÿ â âèäó ïðåèìóùåñòâåííî ïîäòâåðæäåíèå âûâîäîâ, ñäåëàííûõ ðàíåå î çàêîíîìåðíîñòÿõ ðàçâèòèÿ ìàòåìàòèêè êàê òåîðèè.
Ìàòåìàòèêà êàê òåîðèÿ ïîëó÷èëà ðàçâèòèå â øêîëå Ïèôàãîðà (571–479 ãã. äî í. ý.).
Ãëàâíîé çàñëóãîé ïèôàãîðåéöåâ â îáëàñòè íàóêè ÿâëÿåòñÿ ñóùåñòâåííîå ðàçâèòèå ìàòåìàòèêè êàê ïî ñîäåðæàíèþ, òàê è ïî ôîðìå. Ïî ñîäåðæàíèþ — îòêðûòèå íîâûõ ìàòåìàòè÷åñêèõ ôàêòîâ. Ïî ôîðìå — ïîñòðîåíèå ãåîìåòðèè è àðèôìåòèêè êàê òåîðåòè÷åñêèõ, äîêàçàòåëüíûõ íàóê, èçó÷àþùèõ ñâîéñòâà îòâëå÷åííûõ ïîíÿòèé î ÷èñëàõ è ãåîìåòðè÷åñêèõ ôîðìàõ.
Äåäóêòèâíîå ïîñòðîåíèå ãåîìåòðèè ÿâèëîñü ìîùíûì ñòèìóëîì å¸ äàëüíåéøåãî ðîñòà.
Ïèôàãîðåéöû ðàçâèëè è îáîñíîâàëè ïëàíèìåòðèþ ïðÿìîëèíåéíûõ ôèãóð: ó÷åíèå î ïàðàëëåëüíûõ ëèíèÿõ, òðåóãîëüíèêàõ, ÷åòûðåõóãîëüíèêàõ, ïðàâèëüíûõ ìíîãîóãîëüíèêàõ. Ïîëó÷èëà ðàçâèòèå ýëåìåíòàðíàÿ òåîðèÿ îêðóæíîñòè è êðóãà. Íàëè÷èå ó ïèôàãîðåéöåâ ó÷åíèÿ î ïàðàëåëüíûõ ëèíèÿõ ãîâîðèò î òîì, ÷òî îíè âëàäåëè ìåòîäîì äîêàçàòåëüñòâà îò ïðîòèâíîãî è âïåðâûå äîêàçàëè òåîðåìó î ñóììå óãëîâ òðåóãîëüíèêà. Âåðøèíîé äîñòèæåíèé ïèôàãîðåéöåâ â ïëàíèìåòðèè ÿâëÿåòñÿ äîêàçàòåëüñòâî òåîðåìû Ïèôàãîðà. Ïîñëåäíÿÿ çà ìíîãî ñòîëåòèé ðàíüøå áûëà ñôîðìóëèðîâàíà âàâèëîíñêèìè, êèòàéñêèìè è èíäèéñêèìè ó÷åíûìè, îäíàêî å¸ äîêàçàòåëüñòâî èì íå áûëî èçâåñòíî.
Óñïåõè ïèôàãîðåéöåâ â ñòåðåîìåòðèè áûëè çíà÷èòåëüíûìè. Îíè çàíèìàëèñü èçó÷åíèåì ñâîéñòâ øàðà, îòêðûëè ïîñòðîåíèå ÷åòûðåõ ïðàâèëüíûõ ìíîãîóãîëüíèêîâ — òåòðàýäðà, êóáà, îêòàýäðà è äîäåêàýäðà (èêîñàýäð èññëåäîâàë âïîñëåäñòâèè Ãåýòåò).
Îäíàêî îíè íå ñìîãëè îáîñíîâàòü óòâåðæäåíèÿ, îòíîñÿùèåñÿ ê îáúåìàì òåë (ïèðàìèäû, êîíóñà, öèëèíäðà è øàðà), õîòÿ, êîíå÷íî, ýòè óòâåðæäåíèÿ áûëè óñòàíîâëåíû ýìïèðè÷åñêè ìíîãî âåêîâ ðàíüøå. Íå çíàëè ïèôàãîðåéöû è îòíîøåíèÿ ïîâåðõíîñòè øàðà ê áîëüøîìó êðóãó.  îáëàñòè àðèôìåòèêè ïèôàãîðåéöû èçó÷àëè ñâîéñòâà ÷åòíûõ è íå÷åòíûõ, ïðîñòûõ è ñîñòàâíûõ íàòóðàëüíûõ ÷èñåë, èñêàëè ñîâåðøåííûå ÷èñëà, ò. å. òàêèå, êîòîðûå ðàâíû ñóììå âñåõ ñâîèõ äåëèòåëåé (íàïðèìåð, 6=1+2+3; 28=1+2+4+7+14). Ïî âèäèìîìó, îíè óñòàíîâèëè, ÷òî åñëè ÷èñëî 2ï
–1 ÿâëÿåòñÿ ïðîñòûì, òî ÷èñëî 2ï–1
´(2ï
–1) — ñîâåðøåííîå. Ïèôàãîðåéöû çíàëè òàêæå äðîáíûå ÷èñëà è â ýòîé ñâÿçè ðàçðàáîòàëè òåîðèþ àðèôìåòè÷åñêîé è ãåîìåòðè÷åñêîé ïðîïîðöèé. Îíè âëàäåëè ïîíÿòèÿìè ñðåäíåãî àðèôìåòè÷åñêîãî, ñðåäíåãî ãåîìåòðè÷åñêîãî è ñðåäíåãî ãàðìîíè÷åñêîãî.
Êàê íè âåëèêè çàñëóãè ïèôàãîðåéöåâ â ðàçâèòèè ñîäåðæàíèÿ è ñèñòåìàòèçàöèè ãåîìåòðèè è àðèôìåòèêè, îäíàêî âñå îíè íå ìîãóò ñðàâíèòüñÿ ñî ñäåëàííûì èìè æå îòêðûòèåì íåñîèçìåðèìûõ âåëè÷èí. Ýòî îòêðûòèå ÿâèëîñü ïîâîðîòíûì ïóíêòîì â èñòîðèè àíòè÷íîé ìàòåìàòèêè.
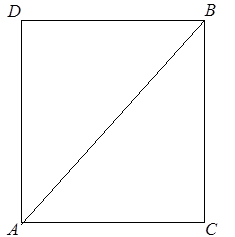
Ïî ïîâîäó ýòîãî îòêðûòèÿ Àðèñòîòåëü ãîâîðèë, ÷òî Ïèôàãîð ïîêàçàë, ÷òî åñëè áû äèàãîíàëü êâàäðàòà áûëà áû ñîèçìåðèìà ñ åãî ñòîðîíîé, òî ÷åòíîå ðàâíÿëîñü áû íå÷åòíîìó.
 Ðèñ. 1 Ðèñ. 1 |
Ýòî çàìå÷àíèå Àðèñòîòåëÿ ÿñíî ïîêàçûâàåò, ÷òî ïðè äîêàçàòåëüñòâå íåñîèçìåðèìîñòè äèàãîíàëè êâàäðàòà ñ åãî ñòîðîíîé Ïèôàãîð èñïîëüçîâàë ìåòîä îò ïðîòèâíîãî (ðèñ. 1).
Ïóñòü, äåéñòâèòåëüíî, äèàãîíàëü ÀÂ
ñîèçìåðèìà ñî ñòîðîíîé ÀÑ
êâàäðàòà ÀÑÂÄ
.
Òîãäà 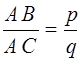 , ãäå ð
è q
— íàòóðàëüíûå ÷èñëà. Äðîáü , ãäå ð
è q
— íàòóðàëüíûå ÷èñëà. Äðîáü 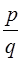 ìîæíî ñ÷èòàòü íåñîêðàòèìîé (èíà÷å å¸ ìîæíî áûëî áû ñîêðàòèòü); çíà÷èò, ð
èëè q
áóäåò ÷èñëîì íå÷åòíûì. ìîæíî ñ÷èòàòü íåñîêðàòèìîé (èíà÷å å¸ ìîæíî áûëî áû ñîêðàòèòü); çíà÷èò, ð
èëè q
áóäåò ÷èñëîì íå÷åòíûì.
Ïðèìåì ÀÑ
=1. Ïî òåîðåìå Ïèôàãîðà äîëæíî áûòü:
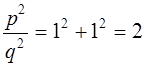 ; ;
Çíà÷èò
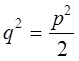 , ,
ò. å. ð
2
äåëèòñÿ íàöåëî íà 2; ñëåäîâàòåëüíî è ð
òàêæå äåëèòñÿ íàöåëî íà 2:
ð=2ð
1
,
ãäå ð
1
— íåêîòîðîå íàòóðàëüíîå ÷èñëî.
Àíàëîãè÷íî ïîëó÷àåì:
q=2q
1
,
ãäå q
1
òàêæå íåêîòîðîå íàòóðàëüíîå ÷èñëî.
Èòàê, ð
è q
— îáà ÷åòíûå ÷èñëà. Ïîñêîëüêó ð
èëè q
— ÷èñëî íå÷åòíîå, âûõîäèò, ÷òî ÷åòíîå ÷èñëî ðàâíî íå÷åòíîìó ÷èñëó.  êîíöå V âåêà äî í. ý. Ôåîäîð èç Êèðåíû óñòàíîâèë, ÷òî íåñîèçìåðèìîñòü äèàãîíàëè êâàäðàòà ñ åãî ñòîðîíîé íå ÿâëÿåòñÿ èñêëþ÷åíèåì. Îí ïîêàçàë, ÷òî ñòîðîíû êâàäðàòîâ, ïëîùàäè êîòîðûõ ðàâíû 3, 5, 6, …, 17 íåñîèçìåðèìû ñî ñòîðîíîé åäèíè÷íîãî êâàäðàòà. Ïèôàãîð ó÷èë, ÷òî ñóùíîñòü âñåõ âåùåé åñòü ÷èñëî; ÷èñëî — ñàìè âåùè; ãàðìîíèÿ ÷èñåë — ãàðìîíèÿ ñàìèõ âåùåé. Àðèñòîòåëü ãîâîðèë, ÷òî ó ïèôàãîðåéöåâ ÷èñëà ïðèíèìàëèñü çà íà÷àëî è â êà÷åñòâå ìàòåðèè è â êà÷åñòâå [âûðàæåíèÿ äëÿ] èõ ñîñòîÿíèÿ è ñâîéñòâ.
Îòêðûòèå íåñîèçìåðèìûõ âåëè÷èí ñíà÷àëà “âûçâàëî óäèâëåíèå” (Àðèñòîòåëü). Ýòî åñòåñòâåííî: äî îòêðûòèÿ Ïèôàãîðà äðåâíåãðå÷åñêèå ìàòåìàòèêè ñ÷èòàëè, ÷òî ëþáûå äâà îòðåçêà èìåþò îáùóþ ìåðó, õîòÿ, ìîæåò áûòü, è î÷åíü ìàëóþ. Êîãäà, îäíàêî, ïèôàãîðåéöû óáåäèëèñü, ÷òî äîêàçàòåëüñòâî ñóùåñòâîâàíèÿ íåñîèçìåðèìûõ âåëè÷èí áåçóïðå÷íî, îíè ïîíÿëè, ÷òî èõ ôèëîñîôèÿ îêàçàëàñü â çàòðóäíèòåëüíîì ïîëîæåíèè.
Ïèôàãîðåéöû çíàëè òîëüêî ïîëîæèòåëüíûå öåëûå è äðîáíûå ÷èñëà. Ñëåäóÿ ñâîåé ôèëîñîôñêîé óñòàíîâêå, îíè, ïî ñóòè äåëà, ñ÷èòàëè, ÷òî êàæäàÿ âåùü ìîæåò áûòü îõàðàêòåðèçîâàíà ïîëîæèòåëüíûì öåëûì èëè äðîáíûì ÷èñëîì, êîòîðîå “âûðàæàåò ñóùíîñòü” ýòîé âåùè. Íà äåëå ýòî îçíà÷àëî, ÷òî ãåîìåòðèÿ ñòðîèëàñü íà áàçå àðèôìåòèêè. Îòêðûòèå íåñîèçìåðèìûõ îòðåçêîâ çíàìåíîâàëî ïîýòîìó íà÷àëî êðèçèñà ïèôàãîðåéñêîé ôèëîñîôèè è ìåòîäîëîãè÷åñêèõ îñíîâ ðàçâèâàåìîé èìè ñèñòåìû ìàòåìàòèêè. Ïîñëå îáíàðóæåíèÿ ñóùåñòâîâàíèÿ íåñîèçìåðèìûõ âåëè÷èí ïåðåä ïèôàãîðåéöàìè îòêðûëèñü äâå âîçìîæíîñòè. Ìîæíî áûëî ïîïûòàòüñÿ ðàñøèðèòü ïîíÿòèå ÷èñëà çà ñ÷åò ïðèñîåäèíåíèÿ ê ðàöèîíàëüíûì ÷èñëàì ÷èñåë èððàöèîíàëüíûõ, îõàðàêòåðèçîâàòü íåñîèçìåðèìûå âåëè÷èíû ÷èñëàìè èíîé ïðèðîäû è òàêèì îáðàçîì âîññòàíîâèòü ñèëó ôèëîñîôñêîãî ïðèíöèïà “âñå åñòü ÷èñëî”.
Îäíàêî, ýòîò ïóòü ñòîëü åñòåñòâåííûé è ïðîñòîé ñ ñîâðåìåííîé òî÷êè çðåíèÿ, äëÿ ïèôàãîðåéöåâ áûë çàêðûò.  ýòîì ñëó÷àå íàäî áûëî ïîñòðîèòü äîñòàòî÷íî ñòðîãóþ àðèôìåòè÷åñêóþ òåîðèþ äåéñòâèòåëüíûõ ÷èñåë, ÷òî ïðè óðîâíå ïèôàãîðåéñêîé ìàòåìàòèêè áûëî äåëîì íåâûïîëíèìûì. Ïîýòîìó íàäî áûëî èäòè ïî äðóãîìó ïóòè — ïî ïóòè îïðåäåëåííîãî ïåðåñìîòðà èñõîäíûõ ïðèíöèïîâ, íàïðèìåð ïðèíÿòü, ÷òî ãåîìåòðè÷åñêèå îáúåêòû ÿâëÿþòñÿ âåëè÷èíàìè áîëåå îáùåé ïðèðîäû, ÷åì äðîáíûå è öåëûå ÷èñëà, è ïûòàòüñÿ ñòðîèòü âñþ ìàòåìàòèêó íå íà àðèôìåòè÷åñêîé, à íà ãåîìåòðè÷åñêîé îñíîâå. Èìåííî ýòîò âòîðîé ïóòü è èçáðàëè ïèôàãîðåéöû, à âñëåä çà íèìè áîëüøèíñòâî äðåâíåãðå÷åñêèõ ìàòåìàòèêîâ, âïëîòü äî Àðõèìåäà è Àïîëëîíèÿ.
 äðåâíåãðå÷åñêîé ôèëîñîôèè ïîíÿòèå áåñêîíå÷íîñòè ïîÿâèëîñü âïåðâûå ó ìàòåðèàëèñòîâ ìèëåòñêîé øêîëû. Àíàêñèìàíäð (610–546 ãã. äî í. ý.), ïåðååìíèê Ôàëåñà, ó÷èë: ìàòåðèÿ áåñêîíå÷íà â ïðîñòðàíñòâå è âî âðåìåíè; âñåëåííàÿ áåñêîíå÷íà, ÷èñëî ìèðîâ áåñêîíå÷íî. Àíàêñèìåí (546 ã. äî í. ý. — ðàñöâåò äåÿòåëüíîñòè) ãîâîðèë: âå÷íûé êðóãîâîðîò ìàòåðèè — ýòî è åñòü áåñêîíå÷íîñòü.
Ïîíÿòèå áåñêîíå÷íîñòè êàê ìàòåìàòè÷åñêàÿ êàòåãîðèÿ âïåðâûå ïîÿâëÿåòñÿ ó Àíàêñèãîðà (îêîëî 500–428 ãã. äî í. ý.).  ñî÷èíåíèè “Î ïðèðîäå” Àíàêñèãîð ïèñàë: âåùè áåñêîíå÷íî äåëèìû, íåò ïîñëåäíåé ñòóïåíè äåëèìîñòè ìàòåðèè; ñ äðóãîé ñòîðîíû, âñåãäà èìååòñÿ íå÷òî áîëüøåå, ÷òî ÿâëÿåòñÿ áîëüøèì.
Áåñêîíå÷íîñòü äëÿ Àíàêñîãîðà — ïîòåíöèàëüíàÿ; îíà ñóùåñòâóåò â äâóõ ôîðìàõ: êàê áåñêîíå÷íî ìàëîå è áåñêîíå÷íî áîëüøîå.  ìàòåìàòèêå òî÷êà çðåíèÿ Àíàêñàãîðà íàøëà áëàãîïðèÿòíóþ ïî÷âó áëàãîäàðÿ îòêðûòèþ íåñîèçìåðèìûõ âåëè÷èí — âåëè÷èí, êîòîðûå íå ìîãóò áûòü èçìåðåíû ëþáîé, êàêîé óãîäíî ìàëîé, îáùåé ìåðîé.
Äåìîêðèò (îêîëî 560–570 ãã. äî í. ý.), ïî-âèäèìîìó, èçó÷àë òàê íàçûâàåìûå ðîãîâèäíûå óãëû (óãëû, îáðàçóåìûå äóãîé îêðóæíîñòè è êàñàòåëüíîé ê íåé).
Ïîñêîëüêó êàæäûé ðîãîâèäíûé óãîë “ìåíüøå” ëþáîãî ïðÿìîëèíåéíîãî óãëà, çäåñü ïîÿâëÿåòñÿ ïîíÿòèå àêòóàëüíî áåñêîíå÷íî ìàëîãî. Âïîñëåäñòâèè ïîÿâèëîñü è ïîíÿòèå àêòóàëüíîé áåñêîíå÷íîñòè.
Àðèñòîòåëü (384–322 ãã. äî í. ý.) îò÷åòëèâî ðàçëè÷àåò äâà âèäà áåñêîíå÷íîñòè: ïîòåíöèàëüíóþ è àêòóàëüíóþ. Ïîíÿòèå àêòóàëüíîé áåñêîíå÷íîñòè â äðåâíåé Ãðåöèè íå ïîëó÷èëî ðàçâèòèÿ êàê â ôèëîñîôèè, òàê è â ìàòåìàòèêå. Ìàòåìàòèêè ñ÷èòàëè, ÷òî “öåëîå áîëüøå ëþáîé ñâîåé ÷àñòè” è, òåì ñàìûì, ïî ñóùåñòâó, èñêëþ÷àëè àêòóàëüíóþ áåñêîíå÷íîñòü. Ôèëîñîôû (Àðèñòîòåëü, íàïðèìåð) äîêàçûâàëè ïðîòèâîðå÷èâîñòü ïîíÿòèÿ àêòóàëüíîé áåñêîíå÷íîñòè è òåì ñàìûì ïîääåðæèâàëè ìàòåìàòèêîâ.
Ïîíÿòèå áåñêîíå÷íîñòè ïîäâåðãàëîñü ñåðüåçíîé êðèòèêå ñî ñòîðîíû Çåíîíà Ýëåéñêîãî (îêîëî 490–430 ãã. äî í. ý.). Çåíîí áûë ó÷åíèêîì Ïàðìåíèäà, ãëàâû ýëåéñêîé øêîëû. Ïàðìåíèä óòâåðæäàë, ÷òî áûòèå åäèíî, íåïîäâèæíî è íåèçìåííî. Äâèæåíèå, èçìåíåíèå — ýòî òîëüêî âèäèìîñòü, îáóñëîâëåííàÿ íåñîâåðøåíñòâîì íàøèõ îðãàíîâ ÷óâñòâ. Ìèð (áûòèå) ìîæåò áûòü ïîçíàí òîëüêî ðàçóìîì, íî íå ÷óâñòâàìè.
Çåíîí Ýëåéñêèé âûäâèíóë 45 àïîðèé (àíòèíîìèé), èìåÿ ïðè ýòîì öåëüþ ðàçâèòü è ëó÷øå îáîñíîâàòü ó÷åíèå Ïàðìåíèäà. Èç ýòèõ àíòèíîìèé äî íàøåãî âðåìåíè äîøëî òîëüêî 9. Âîò íàèáîëåå õàðàêòåðíûå èç íèõ.
Ïðîòèâ äâèæåíèÿ.
“Дихотомия”.
Äâèæåíèÿ íåò, ïîòîìó ÷òî òî, ÷òî äâèæåòñÿ, äîëæíî äîéòè äî ñåðåäèíû, ïðåæäå ÷åì îíî äîéäåò äî êîíöà. Íî åñëè áû òåëî äîøëî äî ñåðåäèíû, îíî äîëæíî áûëî áû ðàíüøå äîéòè äî ñåðåäèíû ýòîé ñåðåäèíû è ò. ä. äî áåñêîíå÷íîñòè, à ýòî íåâîçìîæíî. Òàêèì îáðàçîì äâèæåíèå íå ìîæåò íà÷àòüñÿ.
“Ахиллес и черепаха”.
Ìåäëåííûé â áåãå íèêîãäà íå áóäåò ïåðåãíàí áûñòðûì, ïîòîìó ÷òî òîò, êòî ïðåñëåäóåò, äîëæåí ñíà÷àëà äîñòè÷ü òî÷êè, èç êîòîðîé íà÷àë óáåãàþùèé, òàê ÷òî óáåãàþùèé âñåãäà áóäåò íà íåêîòîðîì ðàññòîÿíèè âïåðåäè.
Çàñëóãà Çåíîíà Ýëåéñêîãî â ðàçâèòèè ôèëîñîôèè è ìàòåìàòèêè ñîñòîèò â òîì, ÷òî îí âûÿâèë ðåàëüíóþ ïðîòèâîðå÷èâîñòü âðåìåíè, äâèæåíèÿ è ïðîñòðàíñòâà, à çíà÷èò è áåñêîíå÷íîñòü. Â. È. Ëåíèí ïèñàë, ÷òî Çåíîí íå îòðèöàë ÷óâñòâåííóþ äîñòîâåðíîñòü äâèæåíèÿ; åãî èíòåðåñîâàë âîïðîñ, êàê âûðàçèòü ñóùíîñòü äâèæåíèÿ â ëîãèêå ïîíÿòèé.
Îäíàêî, Çåíîí ïîñëåäíþþ çàäà÷ó íå ðåøèë, íå ðåøèëè å¸ è äðóãèå ó÷åíûå äðåâíåé Ãðåöèè.
 ðàçâèòèè ñîäåðæàíèÿ è ñïîñîáîâ îáîñíîâàíèÿ ìàòåìàòèêè äðåâíåé Ãðåöèè âûäàþùóþñÿ ðîëü ñûãðàëè òðè çàäà÷è: òðèñåêöèÿ óãëà, óäâîåíèå êóáà (äåëèéñêàÿ çàäà÷à) è êâàäðàòóðà êðóãà.
Ïðîáóæäåíèå îñîáîãî èíòåðåñà ê ýòèì çàäà÷àì èìåííî â äðåâíåé Ãðåöèè íå ñëó÷àéíî. Ïðè ïîñòðîåíèè ìàòåìàòèêè êàê äåäóêòèâíîé ñèñòåìû, áàçèðóþùåéñÿ íà ãåîìåòðè÷åñêîì ôóíäàìåíòå äâå ïåðâûå çàäà÷è ïîÿâëÿþòñÿ êàê åñòåñòâåííûå îáîáùåíèÿ áîëåå ýëåìåíòàðíûõ çàäà÷. Çàäà÷à î êâàäðàòóðå êðóãà áûëà ïîëó÷åíà “ïî íàñëåäñòâó” îò äðåâíèõ åãèïòÿí è âàâèëîíÿí.
Трисекция угла. Äàí ÐÀÂÑ
, òðåáóåòñÿ ðàçäåëèòü åãî íà òðè ðàâíûå ÷àñòè. Ôîðìóëèðîâêà çàäà÷è îòíîñèòñÿ ê ëþáîìó óãëó è ÿâëÿåòñÿ îáîáùåíèåì çàäà÷è î äåëåíèè äàííîãî óãëà íà äâå ðàâíûå ÷àñòè.
 Ðèñ. 2 Ðèñ. 2 |
Удвоение куба. Ïîñòðîèòü êóá, îáúåì êîòîðîãî â äâà ðàçà áîëüøå îáúåìà äàííîãî êóáà. Ïîñòðîèòü êâàäðàò, ïëîùàäü êîòîðîãî â äâà ðàçà áîëüøå ïëîùàäè äàííîãî êâàäðàòà. Åñëè ñòîðîíà äàííîãî êâàäðàòà à
, à èñêîìîãî õ
, òî õ
2
=2à
2
;  . Ñëåäîâàòåëüíî, ñòîðîíà èñêîìîãî êâàäðàòà ðàâíà äèàãîíàëè äàííîãî. Îòñþäà îñóùåñòâèìîñòü ïîñòðîåíèÿ öèðêóëåì è ëèíåéêîé èñêîìîãî êâàäðàòà AA`CC`
(ðèñ. 2). . Ñëåäîâàòåëüíî, ñòîðîíà èñêîìîãî êâàäðàòà ðàâíà äèàãîíàëè äàííîãî. Îòñþäà îñóùåñòâèìîñòü ïîñòðîåíèÿ öèðêóëåì è ëèíåéêîé èñêîìîãî êâàäðàòà AA`CC`
(ðèñ. 2).
Âïîëíå åñòåñòâåííî áûëî ïåðåéòè îò ýòîé çàäà÷è íà ïëîñêîñòè ê ñîîòâåòñòâóþùåé çàäà÷è â ïðîñòðàíñòâå: ïîñòðîèòü êóá, îáúåì êîòîðîãî â äâà ðàçà áîëüøå îáúåìà äàííîãî êóáà.
Квадратура круга. Ïîñòðîèòü êâàäðàò, ïî ïëîùàäè ðàâíûé äàííîìó êðóãó.
Íè îäíà èç óêàçàííûõ çàäà÷ íå ðàçðåøèìà öèðêóëåì è ëèíåéêîé.
Ïèôàãîðåéöû çàëîæèëè îñíîâû ãåîìåòðè÷åñêîé àëãåáðû. Òåýòåò è Åâêëèä óñòàíîâèëè êëàññèôèêàöèþ êâàäðàòè÷íûõ èððàöèîíàëüíîñòåé.
Åâäîïñ ðàçâèë îáùóþ òåîðèþ ïðîïîðöèé — ãåîìåòðè÷åñêèé ýêâèâàëåíò òåîðèè ïîëîæèòåëüíûõ âåùåñòâåííûõ ÷èñåë — è ðàçðàáîòàë ìåòîä èñ÷åðïûâàíèÿ — çà÷àòî÷íóþ ôîðìó òåîðèè ïðåäåëîâ, îñíîâàííóþ íà ãåîìåòðè÷åñêîé áàçå. Ýòè òåîðèè ñîçäàëè ïðî÷íûé êàðêàñ çäàíèÿ äðåâíåãðå÷åñêîé ìàòåìàòèêè, ôóíäàìåíòîì êîòîðîãî áûëà ãåîìåòðèÿ; òåì ñàìûì ïðåîäîëåâàëèñü òðóäíîñòè, ñâÿçàííûå ñ ôàêòîì ñóùåñòâîâàíèÿ íåñîèçìåðèìûõ âåëè÷èí.
×òîáû èçáåæàòü òðóäíîñòåé â îáîñíîâàíèè ìàòåìàòèêè, ñâÿçàííûõ ñ ïàðàäîêñàìè áåñêîíå÷íîñòè (Çåíîí, Àðèñòîòåëü), áîëüøèíñòâî ó÷åíûõ äðåâíåé Ãðåöèè ïðåäïî÷ëè îòêàçàòüñÿ îò èñïîëüçîâàíèÿ â ìàòåìàòèêå èäåé áåñêîíå÷íîñòè è äâèæåíèÿ èëè ñâåñòè èõ ïðèìåíåíèå ê ìèíèìóìó.  êà÷åñòâå òàêîãî ìèíèìóìà áûëî ïðèíÿòî óòâåðæäåíèå î íåîãðàíè÷åííîé äåëèìîñòè ãåîìåòðè÷åñêèõ âåëè÷èí.
Ðàññìîòðåíèå òðåõ çíàìåíèòûõ çàäà÷ ïðèâåëî äðåâíåãðå÷åñêèõ ó÷åíûõ ê óáåæäåíèþ, ÷òî ðåøåíèå ãåîìåòðè÷åñêîé çàäà÷è ìîæåò ñ÷èòàòüñÿ âûïîëíåííûì ñòðîãî ãåîìåòðè÷åñêè ëèøü ïðè óñëîâèè èñïîëüçîâàíèÿ òîëüêî (èäåàëüíûõ) öèðêóëÿ è ëèíåéêè. Èñïîëüçîâàíèå ìåõàíè÷åñêèõ ñðåäñòâ â ãåîìåòðèè íå äîïóñêàåòñÿ.
Òîëüêî ïîñëå îñíîâîïîëàãàþùèõ ðàáîò ïèôàãîðåéöåâ, Òåýòåòà, Åâäîêñà è äðóãèõ ìàòåìàòèêîâ, ïîñëå ñîãëàøåíèÿ î íåîáõîäèìûõ îãðàíè÷åíèÿõ è äîïóñòèìûõ ñðåäñòâàõ ïîñòðîåíèÿ, Åâêëèä íàïèñàë “Íà÷àëà
”, ïîñâÿùåííûå îñíîâàì è ìåòîäàì äðåâíåãðå÷åñêîé ìàòåìàòèêè.  “Íà÷àëàõ
” Åâêëèäà êðèçèñ îñíîâ äðåâíåãðå÷åñêîé ìàòåìàòèêè áûë ïðåîäîëåí — êîíå÷íî, äëÿ ñâîåãî âðåìåíè, è, äîáàâèì, ïðåîäîëåí íå âî âñåõ ïóíêòàõ è íå âñåãäà ñîâåðøåííûì îáðàçîì.
 êîíöå XVII è â XVIII âåêå âñå âîçðàñòàþùèå çàïðîñû ïðàêòèêè è äðóãèõ íàóê ïîáóæäàëè ó÷åíûõ ìàêñèìàëüíî ðàñøèðÿòü îáëàñòü è ìåòîäû èññëåäîâàíèé ìàòåìàòèêè. Ïîíÿòèÿ áåñêîíå÷íîñòè, äâèæåíèÿ è ôóíêöèîíàëüíîé çàâèñèìîñòè âûäâèãàþòñÿ íà ïåðâîå ìåñòî, ñòàíîâÿòñÿ îñíîâîé íîâûõ ìåòîäîâ ìàòåìàòèêè.
 êîíöå XVII è â XVIII âåêå â ìàòåìàòèêå è ìåõàíèêå áûëè ïîëó÷åíû êëàññè÷åñêèå ðåçóëüòàòû ôóíäàìåíòàëüíîãî çíà÷åíèÿ. Îñíîâíûì çäåñü áûëî ðàçâèòèå äèôôåðåíöèàëüíîãî è èíòåãðàëüíîãî èñ÷èñëåíèÿ, òåîðèè äèôôåðåíöèàëüíûõ óðàâíåíèé, âàðèàöèîííîãî èñ÷èñëåíèÿ è àíàëèòè÷åñêîé ìåõàíèêè. Çíà÷èòåëüíûå ðåçóëüòàòû áûëè ïîëó÷åíû â àëãåáðå è òåîðèè ÷èñåë. À. Ýéëåð, à âñëåä çà íèì è íåêîòîðûå äðóãèå ó÷åíûå âòîðîé ïîëîâèíû XVIII âåêà ïðîäåëàëè áîëüøóþ ðàáîòó ïî ñèñòåìàòèçàöèè ñîäåðæàíèÿ ìàòåìàòè÷åñêèõ äèñöèïëèí, â ïåðâóþ î÷åðåäü ìàòåìàòè÷åñêîãî àíàëèçà, à âìåñòå ñ íèì àëãåáðû è òðèãîíîìåòðèè.
Âìåñòå ñ òåì, â ðàññìàòðèâàåìûé ïåðèîä ñïîñîáû îáîñíîâàíèÿ ìàòåìàòè÷åñêèõ òåîðèé — îñîáåííî äèôôåðåíöèàëüíîãî èñ÷èñëåíèÿ — ðåçêî îòñòàâàëè îò áóðíî ðàçâèâàþùåãîñÿ ñîäåðæàíèÿ ìàòåìàòèêè. Ýòî îòñòàâàíèå ïðîÿâèëîñü â ðàçëè÷íûõ, ìåæäó ñîáîé ñâÿçàííûõ ôîðìàõ è ïðèòîì ñâîåîáðàçíî â îòäåëüíûõ ìàòåìàòè÷åñêèõ òåîðèÿõ.
Îáùåé ÷åðòîé ïîïûòîê îáîñíîâàíèÿ ìàòåìàòèêè ñ êîíöà XVII è ïëàíîìåðíî äî ïîñëåäíåé ÷åòâåðòè XVIII âåêà áûëî ñòðåìëåíèå îáîñíîâàòü êàæäóþ ìàòåìàòè÷åñêóþ òåîðèþ â ïîëíîì ñîîòâåòñòâèè ñ èñòèíàìè ýëåìåíòàðíîé, “íèçøåé” (ïî òåðìèíîëîãèè Ô. Ýíãåëüñà) ìàòåìàòèêè, ò. å. ýëåìåíòàðíîé ìàòåìàòèêè, êàêîé îíà áûëà ïðèìåðíî äî îòêðûòèÿ àíàëèòè÷åñêîé ãåîìåòðèè
. Ýòî ñòðåìëåíèå ïðîÿâèëîñü â äâóõ ôîðìàõ. Ñíà÷àëà ìàòåìàòèêè ïûòàëèñü âîçäâèãíóòü ðàçâèâàåìûå èìè ìàòåìàòè÷åñêèå òåîðèè íà ôóíäàìåíòå, ïîñòðîåííîì â ñâîå âðåìÿ äëÿ îáîñíîâàíèÿ “íèçøåé” ìàòåìàòèêè. Ýòî õîðîøî ïîêàçûâàþò ãîñïîäñòâîâàâøèå â òî âðåìÿ ñïîñîáû îáîñíîâàíèÿ àëãåáðû è ó÷åíèÿ î ÷èñëå. Åñëè æå òàêîå ïîñòðîåíèå ÿâíî íå óäàâàëîñü (÷òî áûëî îñîáåííî ÿñíî â îòíîøåíèè äèôôåðåíöèàëüíîãî èñ÷èñëåíèÿ ñ ìîìåíòà åãî âîçíèêíîâåíèÿ), òî ñòàðàëèñü îáîñíîâàòü ìàòåìàòè÷åñêóþ òåîðèþ íà ïðèíöèïàõ, ñïåöèàëüíî äëÿ íå¸ ðàçðàáîòàííûõ, ñîäåðæàíèå êîòîðûõ ìîæíî ìàêñèìàëüíî ñîãëàñîâàòü, “ïðèìèðèòü” (Ýíãåëüñ) ñ èñòèíàìè “íèçøåé” ìàòåìàòèêè.
Èíà÷å ãîâîðÿ, â îáîèõ ñëó÷àÿõ ïðèíöèïû è óòâåðæäåíèÿ “íèçøåé” ìàòåìàòèêè ìåòàôèçè÷åñêè àáñîëþòèçèðîâàëèñü
, ðàññìàòðèâàëèñü êàê íåçûáëåìûé
ôóíäàìåíò êàæäîé ìàòåìàòè÷åñêîé òåîðèè.
 êîíöå XVII è îñîáåííî â ïåðâûõ òðåõ ÷åòâåðòÿõ XVIII âåêà îñíîâíûå ïîíÿòèÿ è çàêîíû, óñòàíîâëåííûå â îäíîé ìàòåìàòè÷åñêîé òåîðèè ÷àñòî ïåðåíîñèëèñü â íîâûå îáëàñòè èññëåäîâàíèÿ, ñîâåðøåííî ôîðìàëüíî, ò. å. áåç îáîñíîâàíèÿ
.
Çàêîíû àëãåáðû è ìàòåìàòè÷åñêîãî àíàëèçà ôîðìèðîâàëèñü áåç óêàçàíèÿ ïåðåìåííûõ, äëÿ êîòîðûõ îíè ñïðàâåäëèâû, è áåç óêàçàíèÿ ãðàíèö èõ ïðèìåíèìîñòè. Òàêàÿ òðàêòîâêà çàêîíîâ àëãåáðû è ìàòåìàòè÷åñêîãî àíàëèçà, åñòåñòâåííî, ðàñïðîñòðàíÿëàñü è íà îñíîâûâàþùèåñÿ íà íèõ àëãîðèòìû.
Ê ñåðåäèíå XVIII âåêà îïèñàííàÿ òðàêòîâêà çàêîíîâ ìàòåìàòè÷åñêîãî àíàëèçà è àëãåáðû ñòàëà íàñòîëüêî îáùåïðèíÿòîé, ÷òî Ë. Ýéëåð ñ÷åë âîçìîæíûì èñòîëêîâàòü å¸ êàê îñíîâíîé ïðèíöèï ìåòîäîëîãèè àíàëèçà âîîáùå. Ñëó÷èëîñü ýòî ïðè ñëåäóþùèõ îáñòîÿòåëüñòâàõ.
 íà÷àëå XVIII âåêà ìåæäó Ëåéáíèöåì è È. Áåðíóëëè âîçíèê ñïîð î “ïðèðîäå” ëîãàðèôìîâ îòðèöàòåëüíûõ ÷èñåë. È. Áåðíóëëè ïîëàãàë, ÷òî ïðè õ
>0, ln
(–x
)=ln x
, òàê êàê  . .
Ëåéáíèö íå ñîãëàñèëñÿ ñ È. Áåðíóëëè; îí óòâåðæäàë, ÷òî îòðèöàòåëüíîå ÷èñëî èìååò áåñ÷èñëåííîå ìíîæåñòâî ëîãàðèôìîâ, ïðè÷åì âñå îíè — ÷èñëà êîìïëåêñíûå. Ñðåäè äðóãèõ ñâîèõ àðãóìåíòîâ Ëåéáíèö óêàçàë, ÷òî ïðàâèëî äèôôåðåíöèðîâàíèÿ ln x
, óñòàíîâëåííîå äëÿ õ
>0, íå îáÿçàòåëüíî äîëæíî áûòü ñïðàâåäëèâûì è äëÿ ln
(–x
).
Ïðè ïîìîùè îñîáîé àðãóìåíòàöèè Ë. Ýéëåð ðåøèë ñïîð â ïîëüçó Ëåéáíèöà. Îäíàêî óêàçàííûé àðãóìåíò Ëåéáíèöà Ýéëåð ðåøèòåëüíî îòêëîíèë. “Ýòî âîçðàæåíèå,— óêàçûâàë Ýéëåð,— åñëè áû îíî áûëî âåðíî, ïîêîëåáàëî áû îñíîâíîå ïîëîæåíèå âñåãî àíàëèçà, çàêëþ÷àþùååñÿ, â îñíîâíûõ ÷åðòàõ, â îáùíîñòè ïðàâèë è îïåðàöèé, ïðèçíàâàåìûõ ñïðàâåäëèâûìè, êàêîâà áû íè áûëà ïðèðîäà êîëè÷åñòâ, ê êîòîðûì îíè ïðèëàãàþòñÿ”.
Êàê ìû âèäèì, ïîäõîä ìàòåìàòèêîâ â XVIII âåêå ê âûÿñíåíèþ ãðàíèö ïðèëîæèìîñòè ìåòîäîâ ìàòåìàòèêè è òðàêòîâêà å¸ ïðèíöèïîâ áûëè ÿâíî ìåòàôèçè÷åñêèìè.
 XVIII âåêå äîêàçàòåëüñòâî òåîðåì ìàòåìàòè÷åñêîãî àíàëèçà íåðåäêî ïðîâîäèëè, îïèðàÿñü íà ãîñïîäñòâîâàâøèå òîãäà ìåõàíè÷åñêèå è ãåîìåòðè÷åñêèå ïðåäñòàâëåíèÿ. Íà÷àëî øèðîêîìó èñïîëüçîâàíèþ ìåõàíè÷åñêèõ ïðåäñòàâëåíèé êàê áàçû ìàòåìàòè÷åñêîãî àíàëèçà ïîëîæèë Íüþòîí â ñâîåì ó÷åíèè î ôëþåíòàõ è ôëþêñèÿõ. ×òî æå êàñàåòñÿ óêàçàííîãî èñïîëüçîâàíèÿ ãåîìåòðè÷åñêèõ ïðåäñòàâëåíèé, òî ïðîùå âñåãî âûÿñíèòü ñóòü äåëà íà ñëåäóþùåì ïðèìåðå.
 íàøå âðåìÿ òåîðåìà î ïðîõîæäåíèè íåïðåðûâíîé ôóíêöèè ÷åðåç íóëåâîå çíà÷åíèå äîêàçûâàåòñÿ â êëàññè÷åñêîì ìàòåìàòè÷åñêîì àíàëèçå ÷èñòî àíàëèòè÷åñêè ñ èñïîëüçîâàíèåì ïîíÿòèÿ áåñêîíå÷íîãî ìíîæåñòâà.  XVIII âåêå åñëè ýòà òåîðåìà è äîêàçûâàëàñü, òî ÷àùå âñåãî óêàçàíèåì íà òî, ÷òî íåïðåðûâíàÿ êðèâàÿ f(x)
, ñîåäèíÿþùàÿ òî÷êè À
è Â
, ðàñïîëîæåííûå â ïëîñêîñòè ïî ðàçíûå ñòîðîíû îñè ÎÕ
, ñóùåñòâóåò ïî ìåíüøåé ìåðå îäíà òî÷êà ñ àáñöèññîé õ=ñ
, a<c<b
, äëÿ êîòîðîé f(ñ)=
0 (ðèñ. 3).
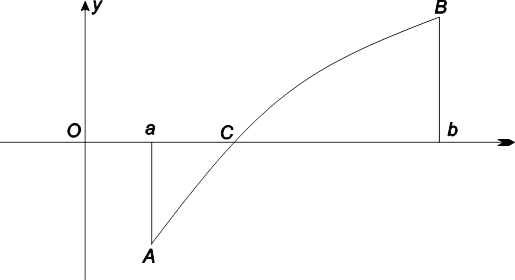
Ðèñ. 3
Ïîäîáíîãî ðîäà ãåîìåòðèçàöèÿ íåðåäêî âñòðå÷àëàñü â ðóêîâîäñòâàõ ïî àëãåáðå è àðèôìåòèêå.
Íàïðèìåð, äîêàçàòåëüñòâî çàêîíà ïåðåìåñòèòåëüíîñòè ab=ba
, ÿêîáû âåðíîãî äëÿ ëþáûõ ÷èñåë è âåëè÷èí, îáû÷íî ñâîäèëè íà äâà ðàâíûõ, íî ðàçëè÷íî ðàñïîëîæåííûõ ïðÿìîóãîëüíèêà (ðèñ. 4).
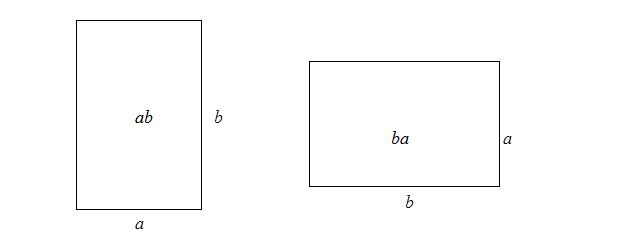
Ðèñ. 4
Ýéëåð è äðóãèå ìàòåìàòèêè XVIII âåêà çàäàâàëè ôóíêöèþ îäíèì àíàëèòè÷åñêèì âûðàæåíèåì è îò ýòîãî àíàëèòè÷åñêîãî âûðàæåíèÿ å¸ íå îòäåëÿëè. Ïðè ýòîì, ïîä àíàëèòè÷åñêèì âûðàæåíèåì, âîîáùå ãîâîðÿ, ïîíèìàëîñü âûðàæåíèå, êîòîðîå ìîæíî ïîëó÷èòü, ñâÿçûâàÿ ýëåìåíòàðíûå ôóíêöèè (àëãåáðàè÷åñêèå è íåêîòîðûå òðàíñöåíäåíòàëüíûå, îäíîãî èëè íåñêîëüêèõ àðãóìåíòîâ) ïîñðåäñòâîì ñëîæåíèÿ, âû÷èòàíèÿ, óìíîæåíèÿ è äåëåíèÿ, âîçâåäåíèÿ â ñòåïåíü è èçâëå÷åíèÿ êîðíÿ, ðåøåíèÿ àëãåáðàè÷åñêèõ óðàâíåíèé è èíòåãðèðîâàíèÿ. Ñ÷èòàëè, ÷òî çàäàíèå ôóíêöèè íà ëþáîì ïðîìåæóòêå îïðåäåëÿåò å¸ ïîâåäåíèå íà âñåé îñè ÎÕ
. Ñîîòâåòñòâåííî ôóíêöèÿ ïðåäñòàâëÿëàñü êðèâîé, ÷àñòè êîòîðîé çàâèñÿò äðóã îò äðóãà è êîòîðóþ ìîæíî çàäàòü îäíèì àíàëèòè÷åñêèì âûðàæåíèåì óêàçàííîãî âèäà. Òàêèå ôóíêöèè ñ÷èòàëè íåïðåðûâíûìè (â ñìûñëå Ýéëåðà), íàçûâàëèñü ïðàâèëüíûìè. Ïðåäñòàâëåííàÿ íà ÷åðòåæå (ðèñ. 5) íåïðåðûâíàÿ â ñîâðåìåííîì ñìûñëå ôóíêöèÿ ó=|õ|
â ñìûñëå Ýéëåðà íå áûëà íåïðåðûâíîé. Äåéñòâèòåëüíî, åñëè èñïîëüçîâàòü çàïàñ ôóíêöèé, ñ êàêèì ðàáîòàëè â XVIII âåêå, òî ýòà ôóíêöèÿ äîëæíà áûòü çàäàíà äâóìÿ ôîðìóëàìè:
f(x)=x, 0
£x;
f(x)=–x, x
£0.
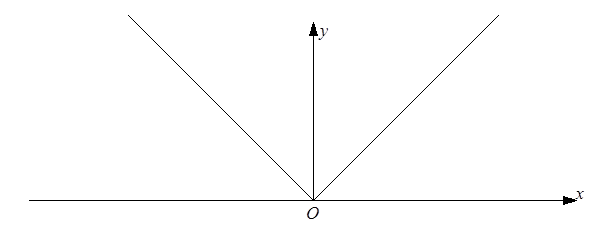
Ðèñ. 5
Âìåñòå ñ äðóãèìè ìàòåìàòèêàìè XVIII âåêà Ýéëåð ñ÷èòàë, ÷òî òàêîå òîëêîâàíèå ôóíêöèè è å¸ íåïðåðûâíîñòè äîñòàòî÷íû äëÿ èíòåãðàëüíîãî è äèôôåðåíöèàëüíîãî èñ÷èñëåíèÿ è òåîðèè îáûêíîâåííûõ äèôôåðåíöèàëüíûõ óðàâíåíèé. Íî âîïðåêè èì îí ïîëàãàë âîçìîæíûì ðàññìàòðèâàòü â òåîðèè óðàâíåíèé ñ ÷àñòíûìè ïðîèçâîäíûìè è ôóíêöèè, çàäàíèå êîòîðûõ íà îòðåçêå íå îïðåäåëÿåò èõ ïîâåäåíèÿ â öåëîì, ò. å. â åãî òåðìèíàõ ïðîèçâîëüíûå
ôóíêöèè. Ýéëåð òðàêòîâàë íåïðåðûâíîñòü òàêèõ ôóíêöèé â ñîâðåìåííîì ñìûñëå è íàçûâàë èõ ñâÿçíûìè. Ê òàêîìó ðàñøèðåíèþ ïîíÿòèÿ ôóíêöèè Ýéëåð ïðèøåë â ñâÿçè ñ àíàëèçîì ðåçóëüòàòîâ èññëåäîâàíèé (ñâîèõ è äðóãèõ ìàòåìàòèêîâ) î êîëåáëþùèõñÿ ñòðóíàõ.
Ðàññìàòðèâàÿ òîëüêî íåïðåðûâíîå è ìîíîòîííîå
èçìåíåíèå ïåðåìåííûõ — â òî âðåìÿ òàê ïîñòóïàëè â ìåõàíèêå è ãåîìåòðèè,— Íüþòîí, Äàëàìáåð è íåêîòîðûå ìàòåìàòèêè XVIII âåêà òîëêîâàëè ïðåäåë òîëüêî êàê òî, ÷òî ïîðîæäàåòñÿ
ïåðåìåííîé, ôàêòè÷åñêè êàê ïîñëåäíåå
çíà÷åíèå ïåðåìåííîé èëè êàê ïîñëåäíåå îòíîøåíèå ïåðåìåííûõ. Âîïðîñ, äîñòèãàåò ëè ïåðåìåííàÿ ýòîãî ñâîåãî ïîñëåäíåãî çíà÷åíèÿ, èëè ìîæåò ïîäîéòè ê íåìó êàê óãîäíî áëèçêî, íèêàêîé ðîëè íå èãðàåò.  ïðàêòèêå ìàòåìàòè÷åñêîãî àíàëèçà ïðåäåë äåéñòâèòåëüíî èçâëåêàëñÿ èç ïåðåìåííîé êàê å¸ ïîñëåäíåå çíà÷åíèå, êîòîðîå îíà ïðèíèìàåò èëè ìîæåò ïðèíÿòü.  êîíöå XVIII âåêà Ëàçàð Êàðíî íàçûâàåò ïðåäåëîì ïîñëåäíåå çíà÷åíèå ïåðåìåííîé, êîòîðàÿ ê íåìó ïðèáëèæàåòñÿ. Äàæå â 40-õ ãîäàõ ïðîøëîãî ñòîëåòèÿ Â. Â. Áóíèêîâñêèé ñ÷èòàë çàäà÷åé äèôôåðåíöèàëüíîãî èñ÷èñëåíèÿ “óëîâèòü îòíîøåíèÿ èçìåíÿþùèõñÿ ïî èçâåñòíîìó çàêîíó âåëè÷èí â òî ñàìîå ìãíîâåíèå, êîãäà ýòè âåëè÷èíû èñ÷åçàþò
”, ò. å. óëîâèòü ïîñëåäíåå çíà÷åíèå îòíîøåíèÿ ïåðåìåííûõ. Êàê ìû óâèäèì ýòà óçêàÿ (íî âûäàâàåìàÿ çà âñåîáùóþ) òðàêòîâêà ïîíÿòèÿ ïðåäåëà ñûãðàëà îñîáî âàæíóþ ðîëü â ðàçâåðòûâàíèè òðóäíîñòåé îáîñíîâàíèÿ ìàòåìàòè÷åñêîãî àíàëèçà â XVIII è íà÷àëå XIX âåêà.
Ìàòåìàòèêè XVII–XVIII âåêîâ ïîëàãàëè òàêæå, ÷òî ëþáàÿ íåïðåðûâíàÿ ôóíêöèÿ f(x)
â êàæäîé òî÷êå, çà èñêëþ÷åíèåì, áûòü ìîæåò, èõ êîíå÷íîãî ÷èñëà èìååò ïðîèçâîäíóþ f`(x)
. Äëÿ äîêàçàòåëüñòâà ýòîãî çàêëþ÷åíèÿ ÷àñòî ïîëàãàëè âîçìîæíûì ïðåäñòàâèòü íåïðåðûâíóþ ôóíêöèþ êðèâîé, êîòîðàÿ, âîîáùå ãîâîðÿ, â êàæäîé òî÷êå èìååò êàñàòåëüíóþ.
 ïåðâîé ïîëîâèíå XVIII âåêà ïîíÿòèå ÷èñëà îïðåäåëÿëîñü ÷àùå âñåãî ïî Åâêëèäó: ÷èñëî åñòü ñîâîêóïíîñòü åäèíèö. Âî âòîðîé ïîëîâèíå XVIII âåêà ÷èñëî èñòîëêîâûâàåòñÿ ïðåèìóùåñòâåííî êàê ðåçóëüòàò èçìåðåíèÿ îäíîé âåëè÷èíû äðóãîé âåëè÷èíîé òîãî æå ðîäà, ïðèíÿòîé çà åäèíèöó. Íî äàæå ïîñëåäíåå, çíà÷èòåëüíî áîëåå øèðîêîå, èñòîëêîâàíèå ïîíÿòèÿ ÷èñëà íå îõâàòûâàëî âñå â òî âðåìÿ èçâåñòíûå âèäû ÷èñåë. Äîñòàòî÷íî âñïîìíèòü, ÷òî â XVII–XVIII âåêàõ ìàòåìàòèêè çíàëè è ñ óñïåõîì èñïîëüçîâàëè ïîíÿòèå êîìïëåêñíîãî ÷èñëà. Ïîýòîìó, íàðÿäó ñ ïîíÿòèåì ÷èñëà, ïðèáåãàëè ê ïðèáåãàëè ê ïîíÿòèÿì î ïîëîæèòåëüíûõ è îòðèöàòåëüíûõ âåëè÷èíàõ, î ìíèìûõ âåëè÷èíàõ, î âåëè÷èíàõ ðåàëüíûõ è ëîæíûõ è ò. ï.
Àëãåáðà òðàêòîâàëàñü êàê íàóêà, èçó÷àþùàÿ òîëüêî îáùèå ñâîéñòâà îáû÷íûõ àðèôìåòè÷åñêèõ è ãåîìåòðè÷åñêèõ âåëè÷èí.
Ïîëàãàëè, ÷òî êàæäàÿ ãåîìåòðè÷åñêàÿ òåîðèÿ — òðèãîíîìåòðèÿ, àíàëèòè÷åñêàÿ ãåîìåòðèÿ è ò. ï. — ÿâëÿåòñÿ òîëüêî íàäñòðîéêîé íàä ãåîìåòðèåé Åâêëèäà è ïîýòîìó äîëæíà ñòðîèòüñÿ íà ôóíäàìåíòå ïîñëåäíåé.
Êîãäà îïèñàííûå âûøå èñòîëêîâàíèÿ îñíîâíûõ ïîíÿòèé, ïðèíöèïîâ è ìåòîäîâ ìàòåìàòèêè ïîëó÷èëè äîñòàòî÷íî øèðîêîå ðàñïðîñòðàíåíèå, â ìàòåìàòè÷åñêèõ òåîðèÿõ íà÷àëè îáíàðóæèâàòüñÿ ïàðàäîêñû; â íåêîòîðûõ ñëó÷àÿõ äàæå ïðèõîäèëè ê ëîæíûì çàêëþ÷åíèÿì, êîòîðûå, îäíàêî, ñ÷èòàëè èñòèííûìè.
Ïàðàäîêñû (è ëîæíûå çàêëþ÷åíèÿ) îáíàðóæèëèñü âïåðâûå â XVI–XVII âåêàõ â ó÷åíèè î ÷èñëå. Îíè ñîõðàíèëè ñâîþ ñèëó è â XVIII âåêå. Îñíîâîé èõ áûëî òî, ÷òî ïî÷òè äî êîíöà XVIII âåêà áîëüøèíñòâî ìàòåìàòèêîâ ïûòàëèñü ïîñòðîèòü ó÷åíèå î ÷èñëå (âïëîòü äî àðèôìåòèêè êîìïëåêñíûõ ÷èñåë!) íà ôóíäàìåíòå, â ñâîå âðåìÿ ðàçðàáîòàííîì äëÿ àðèôìåòèêè êîëè÷åñòâåííûõ íàòóðàëüíûõ ÷èñåë. Îáû÷íûå, âåðíûå äëÿ êîëè÷åñòâåííûõ íàòóðàëüíûõ ÷èñåë, îïðåäåëåíèÿ àðèôìåòè÷åñêèõ äåéñòâèé è âñå ïÿòü çàêîíîâ ñ÷åòà çàðàíåå ïðè ýòîì ñ÷èòàëèñü ñïðàâåäëèâûìè â êàæäîé îáëàñòè ÷èñåë.  ñâÿçè ñ ýòèì íàõîäÿòñÿ õàðàêòåðíûå äëÿ âòîðîé ïîëîâèíû XVII è XVIII âåêà “äîêàçàòåëüñòâà” ïðàâèëà çíàêîâ (–a)(–b)=+ab;
ñîìíåíèÿ â èñòèííîñòè ïðîïîðöèè +1: –1= –1: +1 (“êàê áîëüøåå, äåëåííîå íà ìåíüøåå, ìîæåò áûòü ðàâíî ìåíüøåìó, äåëåííîìó íà áîëüøåå?”); îòðèöàíèå îáúåêòèâíîñòè ïîíÿòèÿ êîìïëåêñíîãî ÷èñëà è ò. ï.
Îäíàêî, äî íà÷àëà XIX âåêà òðóäíîñòè îáîñíîâàíèÿ ó÷åíèÿ î ÷èñëå íå ìåøàëè óñïåøíîìó èñïîëüçîâàíèþ ïîíÿòèÿ ÷èñëà â ìàòåìàòèêå, òî÷íûõ íàóêàõ è òåõíèêå. Ýòî èìåëî îñíîâàíèåì òî, ÷òî â ëþáîé îáëàñòè ÷èñåë, îò íàòóðàëüíûõ äî êîìïëåêñíûõ, âñå ïÿòü çàêîíîâ ñ÷åòà âûïîëíÿþòñÿ. Êðîìå òîãî, â ýòîò ïåðèîä â ìàòåìàòèêå âåäóùåå ïîëîæåíèå ïðèíàäëåæàëî ìàòåìàòè÷åñêîìó àíàëèçó. Ïîýòîìó âîïðîñû îáîñíîâàíèÿ ó÷åíèÿ î ÷èñëå õîòÿ è îáñóæäàëèñü àêòèâíî, íî â äåëå ðàçðàáîòêè îñíîâ ìàòåìàòèêè èãðàëè âòîðîñòåïåííóþ ðîëü.
Ó÷åíûå è ôèëîñîôû îáðàòèëè ñåðüåçíîå âíèìàíèå íà òðóäíîñòè îáîñíîâàíèÿ ìàòåìàòèêè ëèøü òîãäà, êîãäà Ëåéáíèö è Íüþòîí ðàçâèëè äèôôåðåíöèàëüíîå è èíòåãðàëüíîå èñ÷èñëåíèå.
Ëåéáíèö è åãî ïîñëåäîâàòåëè — áðàòüÿ Áåðíóëëè, Ëîïèíòàëü è äðóãèå — òðàêòîâàëè äèôôåðåíöèàëû êàê áåñêîíå÷íî ìàëûå ðàçíîñòè îáû÷íûõ êîíå÷íûõ âåëè÷èí
, êàê òîãäà ãîâîðèëè — “ðåàëüíûõ” âåëè÷èí. Ïîýòîìó îíè îáðàùàëèñü ñ òåìè è äðóãèìè îäèíàêîâî è â èñ÷èñëåíèè ïðèìåíÿëè ê ïåðâûì òå æå ïðèåìû, êîòîðûå ñïðàâåäëèâû ïðè äåéñòâèÿõ ñî âòîðûìè. Âìåñòå ñ òåì âûÿñíèëîñü, ÷òî òàêèì îáðàçîì òðàêòóåìûì áåñêîíå÷íî ìàëûì ïðèñóùå ñâîéñòâî, ïðîòèâîðå÷àùåå îäíîìó îñíîâíîìó ñâîéñòâó îñíîâíûõ êîíå÷íûõ âåëè÷èí
: åñëè À
— êîíå÷íàÿ âåëè÷èíà, à a
— áåñêîíå÷íî ìàëàÿ, òî, ÷òîáû ðåçóëüòàò èñ÷èñëåíèÿ ïîëó÷àëñÿ ñîâåðøåííî òî÷íûì, îêàçàëîñü íåîáõîäèìûì ïðîâîäèòü âû÷èñëåíèÿ â ïðåäïîëîæåíèè, ÷òî À+
a=À
.
Äèôôåðåíöèàëüíîå èñ÷èñëåíèå, çíà÷åíèå êîòîðîãî äëÿ ðàçâèòèÿ íàóêè è òåõíèêè áûëî âíå ñîìíåíèé, îêàçàëîñü â ïàðàäîêñàëüíîì ïîëîæåíèè: ÷òîáû åãî ìåòîäàìè ïîëó÷èòü òî÷íûé ðåçóëüòàò, íàäî áûëî èñõîäèòü èç îøèáî÷íîãî óòâåðæäåíèÿ.
Íüþòîí ïûòàëñÿ îáîñíîâàòü äèôôåðåíöèàëüíîå èñ÷èñëåíèå íà çàêîíàõ ìåõàíèêè è ïîíÿòèè ïðåäåëà. Íî åìó íå óäàëîñü îñâîáîäèòü ñâîå èñ÷èñëåíèå ôëþêñèé îò íåäîñòàòêîâ, ïðèñóùèõ äèôôåðåíöèàëüíîìó èñ÷èñëåíèþ Ëåéáíèöà.  ïðàêòèêå âû÷èñëåíèÿ Íüþòîí, êàê è Ëåéáíèö, ïðèìåíÿë ïðèíöèï îòáðàñûâàíèÿ áåñêîíå÷íî ìàëûõ.
Ê. Ìàðêñ íàçûâàë äèôôåðåíöèàëüíîå èñ÷èñëåíèå Ëåéáíèöà–Íüþòîíà ìèñòè÷åñêèì
. Ýòèì îí õîòåë â ïåðâóþ î÷åðåäü ïîä÷åðêíóòü, ÷òî Ëåéáíèö è Íüþòîí ââîäèëè â äèôôåðåíöèàëüíîå èñ÷èñëåíèå áåñêîíå÷íî ìàëûå ìåòàôèçè÷åñêè, ñðàçó ïîëàãàÿ èõ ñóùåñòâóþùèìè, áåç âûÿñíåíèÿ èõ âîçíèêíîâåíèÿ è ðàçâèòèÿ è áåç àíàëèçà ïðèðîäû èõ ñïåöèôè÷åñêèõ ñâîéñòâ.
Ïàðàäîêñû âîçíèêëè è â òåîðèè ðÿäîâ. Íàïðèìåð, â XVIII âåêå ïîëàãàëè, ÷òî “ñóììà ðÿäà”
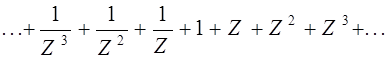
ðàâíà 0, òàê êàê
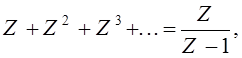
à
 . .
Ìíîãî ñïîðîâ âûçâàë âîïðîñ î “ñóììå” ðÿäà
1–1+1–1…
ïîñêîëüêó, êàê ãîâîðèëè, “ñ îäíîé ñòîðîíû,
(1–1)+(1–1)…=0,
à ñ äðóãîé —
1–(1–1)-(1–1)…=1”.
Ïîïûòêè ïîñòðîèòü àíàëèç áåñêîíå÷íî ìàëûõ è òåîðèþ ðÿäîâ â ïîëíîì ñîîòâåòñòâèè ñ îñíîâíûìè ïîíÿòèÿìè è èñòèíàìè “íèçøåé” ìàòåìàòèêè ñ ñàìîãî íà÷àëà ê óñïåøíûì ðåçóëüòàòàì íå ïðèâåëè. Ïîýòîìó Ëåéáíèö è åãî ïîñëåäîâàòåëè ïûòàëèñü îïðàâäàòü ïðèíöèïû àíàëèçà áåñêîíå÷íî ìàëûõ è òåîðèþ ðÿäîâ òàêæå ïóòåì ñðàâíåíèÿ áåñêîíå÷íî ìàëîé ñ ïåñ÷èíêîé, êîòîðîé ìîæíî ïðåíåáðå÷ü ïðè âû÷èñëåíèè âûñîòû ãîðû, ïîñðåäñòâîì ññûëîê íà âåðîÿòíîñòü è ò. ï.
 XVII–XVIII âåêàõ ïîëó÷èë ðàçâèòèå è äðóãîé ïîäõîä ê “ñîãëàñîâàíèþ” íîâûõ èñòèí ìàòåìàòèêè ñ “âå÷íûìè” èñòèíàìè “íèçøåé” ìàòåìàòèêè. Êîãäà ïîíÿòèÿ ìàòåìàòè÷åñêîé òåîðèè ðåçêî îòëè÷àëèñü îò ðàññìàòðèâàåìûõ â “íèçøåé” ìàòåìàòèêå, îíè îáúÿâëÿëèñü “âîîáðàæàåìûìè” è ðàññìàòðèâàëèñü êàê âñïîìîãàòåëüíûå
ôóíêöèè, íåîáõîäèìûå äëÿ èçó÷åíèÿ ñâîéñòâ îáû÷íûõ êîíå÷íûõ âåëè÷èí. Êðóïíåéøèå ìàòåìàòèêè XVIII âåêà íåîäíîêðàòíî ïûòàëèñü äîêàçàòü, ÷òî ïîíÿòèå êîìïëåêñíîãî ÷èñëà íå äîïóñêàåò íèêàêîãî ðåàëüíîãî èñòîëêîâàíèÿ. Òàêèå æå ïîïûòêè ïðèíèìàëèñü è â îòíîøåíèè ïîíÿòèÿ áåñêîíå÷íî ìàëîé âåëè÷èíû. Íî è íà ýòîì ïóòè óñòàíîâèòü åäèíñòâî ìíåíèé íå óäàëîñü.  ýòî âðåìÿ, êàæäàÿ çàäà÷à, îòíîñÿùàÿñÿ ê âåëè÷èíàì, èçó÷àåìûì â ìåõàíèêå, àñòðîíîìèè, òåõíèêå è ò. ï., åñëè è äîïóñêàëî ðåøåíèå, òî îáû÷íî ïîñëåäíåå âûðàæàëîñü ïðè ïîìîùè äåéñòâèòåëüíûõ ÷èñåë (äåéñòâèòåëüíûõ êîðíåé); êîìïëåêñíûå ÷èñëà (êîìïëåêñíûå êîðíè) óêàçûâàëè íà íåâîçìîæíîñòü å¸ ðåøåíèÿ.  êîíöå XVII è â XVIII âåêå òîëüêî íåñêîëüêî ìàòåìàòèêîâ — Âàëëèñ, Êþí, â êîíöå æèçíè Ýéëåð — ñ÷èòàëè ïîíÿòèå êîìïëåêñíîãî ÷èñëà äîïóñêàþùèì ðåàëüíîå èñòîëêîâàíèå.  êîíöå XVIII âåêà Âåññåëü ðàçðàáîòàë ïîëíîå ãåîìåòðè÷åñêîå èñòîëêîâàíèå àðèôìåòèêè êîìïëåêñíûõ ÷èñåë. Ïî îñíîâíûì ñâîéñòâîì, âàæíûì äëÿ àëãîðèòìîâ àëãåáðû è àíàëèçà, êîìïëåêñíûå ÷èñëà íå îòëè÷àþòñÿ îò ÷èñåë äåéñòâèòåëüíûõ. Ïðåäñòàâëÿëàñü âîçìîæíîñòü îáúÿâèòü êîìïëåêñíûå ÷èñëà “âîîáðàæàåìûìè” è, îáîéäÿ âîïðîñû îáîñíîâàíèÿ èõ àðèôìåòèêè, îñòàâèòü èõ â ìàòåìàòèêå â êà÷åñòâå “ïîëåçíûõ âñïîìîãàòåëüíûõ ôóíêöèé”. Íàïðîòèâ, òðàêòîâêà áåñêîíå÷íî ìàëûõ êàê “ïîëåçíûõ ôóíêöèé” øèðîêîãî ðàñïðîñòðàíåíèÿ íå ïîëó÷èëà: ìàòåìàòèêè çíàëè ìåõàíè÷åñêîå è ãåîìåòðè÷åñêîå èñòîëêîâàíèå dx
è dy
.
Ïðèìåðíî ñ ïîñëåäíåé ÷åòâåðòè XVIII âåêà îáëàñòü ïðèëîæåíèé ìàòåìàòè÷åñêîãî àíàëèçà íà÷èíàåò çíà÷èòåëüíî ïåðåêðûâàòü ãðàíèöû åãî îáû÷íîãî ïðèëîæåíèÿ â ìåõàíèêå è ãåîìåòðèè. Åù¸ áûñòðåå ðàçâåðòûâàåòñÿ ýòîò ïðîöåññ â ïåðâîé ÷åòâåðòè XIX âåêà.
Ìàòåìàòèêè ïûòàëèñü ñíà÷àëà ðåøàòü íîâûå çàäà÷è ìåòîäàìè, ðàçðàáîòàííûìè êëàññèêàìè XVIII âåêà — Ýéëåðîì, Äàëàìáåðîì, Ëàãðàíæåì è äðóãèìè. Îäíàêî, âñêîðå âûÿñíèëîñü, ÷òî ìåòîäû êëàññèêîâ íåäîñòàòî÷íû, ÷òî íàäî ðàçâèâàòü íîâûå, áîëåå îáùèå è ñèëüíûå ìåòîäû. Âûÿñíèëîñü òàêæå, ÷òî íåäîñòàòî÷íîñòü ìåòîäîâ êëàññèêîâ íåðåäêî ñâÿçàíà ñ óçîñòüþ òðàêòîâêè îñíîâíûõ ïîíÿòèé, ñ “èçãîíÿåìûì” ïîíÿòèåì î áåñêîíå÷íî ìàëîì, ñ “èñêëþ÷åíèÿìè”, êîòîðûå ðàíüøå îñòàâàëèñü â òåíè.
Ïîÿñíèì ñêàçàííîå îäíèì ïðèìåðîì.
Íüþòîí è Ëåéáíèö ðàçðàáîòàëè äâå òðàêòîâêè ïîíÿòèÿ îáû÷íîãî îïðåäåëåííîãî èíòåãðàëà.
Íüþòîí òðàêòîâàë îïðåäåëåííûé èíòåãðàë êàê ðàçíîñòü ñîîòâåòñòâóþùèõ çíà÷åíèé ïåðâîîáðàçíîé ôóíêöèè:
 , ,
ãäå F`
(x)=f(x)
.
Äëÿ Ëåéáíèöà îïðåäåëåííûé èíòåãðàë áûë ñóììîé âñåõ áåñêîíå÷íî ìàëûõ äèôôåðåíöèàëîâ.
 . .
Ïåðâàÿ òðàêòîâêà îòâå÷àëà òåõíèêå âû÷èñëåíèÿ îïðåäåëåííûõ èíòåãðàëîâ ïðè ïîìîùè ïåðâîîáðàçíîé ïåðâîîáðàçíîé ïîäûíòåãðàëüíîé ôóíêöèè, âòîðàÿ — ïîòîìó, ÷òî â ïðèëîæåíèÿõ îïðåäåëåííûé èíòåãðàë ïîÿâëÿëñÿ êàê ïðåäåë èçâåñòíîãî âèäà ñóììû (èíòåãðàëüíîé ñóììû).
Ïðèìåðíî äî ïîñëåäíåé ÷åòâåðòè XVIII âåêà ïåðâàÿ òðàêòîâêà ïîíÿòèÿ îïðåäåëåííîãî èíòåãðàëà çàíèìàëà ãîñïîäñòâóþùåå ïîëîæåíèå. Ýòîìó ñïîñîáñòâîâàëè äâà îáñòîÿòåëüñòâà.
Ê íà÷àëó XVIII âåêà áûëè óñòàíîâëåíû ïðàâèëà äèôôåðåíöèðîâàíèÿ âñåõ ýëåìåíòàðíûõ ôóíêöèé è íà÷àëàñü óñïåøíàÿ ðàçðàáîòêà ìåòîäîâ íàõîæäåíèÿ èõ ïåðâîîáðàçíûõ (ðàöèîíàëüíûõ, îòäåëüíûõ êëàññîâ èððàöèîíàëüíûõ è òðàíñöåíäåíòíûõ ôóíêöèé). Áëàãîäàðÿ ýòîìó òî÷êà çðåíèÿ íüþòîíà âïîëíå îòâå÷àëà ðàçâèòèþ ýôôåêòèâíûõ àëãîðèòìîâ èíòåãðàëüíîãî èñ÷èñëåíèÿ.
Íåïîñðåäñòâåííîå âû÷èñëåíèå  êàê ïðåäåëà èíòåãðàëüíîé ñóììû ñòîëêíóëîñü ñ ìíîãèìè òðóäíîñòÿìè. Åñòåñòâåííî, ÷òî ýòî îáñòîÿòåëüñòâî óêðåïëåíèþ òî÷êè çðåíèÿ Ëåéáíèöà íå ñïîñîáñòâîâàëî. êàê ïðåäåëà èíòåãðàëüíîé ñóììû ñòîëêíóëîñü ñ ìíîãèìè òðóäíîñòÿìè. Åñòåñòâåííî, ÷òî ýòî îáñòîÿòåëüñòâî óêðåïëåíèþ òî÷êè çðåíèÿ Ëåéáíèöà íå ñïîñîáñòâîâàëî.
Ëåéáíèöåâî èñòîëêîâàíèå îáû÷íîãî îïðåäåëåííîãî èíòåãðàëà ñóùåñòâåííî îïèðàëîñü íà ïîíÿòèå î áåñêîíå÷íî ìàëûõ, îò êîòîðîãî ìàòåìàòèêè XVIII âåêà õîòåëè îñâîáîäèòü ìàòåìàòè÷åñêèé àíàëèç. Ýòî òàêæå ñïîñîáñòâîâàëî óêðåïëåíèþ òî÷êè çðåíèÿ Íüþòîíà. Ôàêò ýòîò õîðîøî ïîäòâåðæäàëñÿ òåì, êàê Ýéëåð èñïîëüçîâàë ïîíÿòèå îá èíòåãðàëüíîé ñóììå. Ýéëåð íå âîçðàæàë ïðîòèâ ïðèáëèæåííîãî âû÷èñëåíèÿ îïðåäåëåííûõ èíòåãðàëîâ ïðè ïîìîùè ñîîòâåòñòâóþùèõ èíòåãðàëüíûõ ñóìì. Íî ðàññìàòðèâàòü îïðåäåëåííûé èíòåãðàë êàê ïðåäåë èíòåãðàëüíîé ñóììû îí íå ìîã.  ýòîì ñëó÷àå âñå ñëàãàåìûå èíòåãðàëüíîé ñóììû ñòàíîâèëèñü áåñêîíå÷íî ìàëûìè, ò. å., ñ òî÷êè çðåíèÿ Ýéëåðà, áûëè íóëÿìè.
Êîíå÷íî, è äî ïîñëåäíåé ÷åòâåðòè XVIII âåêà êîíöåïöèÿ Íüþòîíà ñòàëêèâàëàñü ñ òðóäíîñòÿìè.  ýòîò ïåðèîä âñòðå÷àëèñü ýëåìåíòàðíûå ôóíêöèè, ïåðâîîáðàçíûå êîòîðûõ íå ìîãóò áûòü âûðàæåíû ÷åðåç ýëåìåíòàðíûå ôóíêöèè. Çíàëè ìàòåìàòèêè è íåêîòîðûå íåñîáñòâåííûå èíòåãðàëû, â òîì ÷èñëå è ðàñõîäÿùèåñÿ. Íî òàêîãî ðîäà ôàêòû áûëè åäèíè÷íûìè è óñòàíîâèâøåéñÿ ýôôåêòèâíîé êîíöåïöèè èíòåãðàëà íàðóøèòü íå ìîãëè. Èíûì îêàçàëîñü ïîëîæåíèå â ïîñëåäíåé ÷åòâåðòè XVIII è îñîáåííî â íà÷àëå XIX âåêà.
Ñ 70-õ ãîäîâ XVIII âåêà ðåøåíèå çàäà÷ àíàëèòè÷åñêîé ìåõàíèêè, ôèçèêè è äðóãèõ äèñöèïëèí ïîòðåáîâàëî çíà÷èòåëüíîå ðàçâèòèå ïîíÿòèÿ îïðåäåëåííîãî èíòåãðàëà. Îñîáîå çíà÷åíèå ïðèîáðåòàþò äâîéíûå è òðîéíûå èíòåãðàëû (Ýéëåð, Ëàãðàíæ, Ëàïëàñ è äð.).
Ðàçðàáîòêà ïðèåìîâ âû÷èñëåíèÿ äâîéíûõ è òðîéíûõ èíòåãðàëîâ ïîêàçàëà, ÷òî âû÷èñëÿòü ýòè èíòåãðàëû òàê, êàê âû÷èñëÿëè îáû÷íûé îïðåäåëåííûé èíòåãðàë — ïðè ïîìîùè íåîïðåäåëåííîãî, î÷åíü òðóäíî èëè äàæå íåâîçìîæíî. Ïîýòîìó ìàòåìàòèêè âûíóæäåíû áûëè ñîõðàíÿòü êîíöåïöèþ Íüþòîíà òîëüêî íà ñëîâàõ, à íà äåëå, ïðè ðåøåíèè çàäà÷ òî÷íûõ íàóê, ñòàëè íà ïóòü Ëåéáíèöà. Îíè âû÷èñëÿëè ñîîòâåòñòâóþùèå èíòåãðàëüíûå ñóììû (â ïðÿìîóãîëüíûõ, öèëèíäðè÷åñêèõ è ñôåðè÷åñêèõ êîîðäèíàòàõ) è íàõîäèëè èõ ïðåäåëû.
Êîðî÷å ãîâîðÿ, ðàçðàáîòêà ñïîñîáîâ âû÷èñëåíèÿ íîâûõ âèäîâ îïðåäåëåííîãî èíòåãðàëà ïîêàçàëà, ÷òî îáûêíîâåííûé, äâîéíîé è ò. ä. îïðåäåëåííûé èíòåãðàëû äîëæíû áûòü îáîñíîâàíû ñàìè ïî ñåáå íåçàâèñèìî îò ïîíÿòèÿ íåîïðåäåëåííîãî èíòåãðàëà. Íî êàæäîå ñëàãàåìîå ëþáîé èíòåãðàëüíîé ñóììû ÿâëÿåòñÿ áåñêîíå÷íî ìàëîé âåëè÷èíîé. Òåì ñàìûì íå òîëüêî ñòàâèëñÿ âîïðîñ î ëåãàëèçàöèè ðàíåå “èçãîíÿåìîãî” ïîíÿòèÿ áåñêîíå÷íî ìàëîãî, íî è î ðàñêðûòèè åãî ðåàëüíîãî ñîäåðæàíèÿ è î ñîîòâåòñòâóþùåì åãî èñïîëüçîâàíèè. Êàê óæå óêàçûâàëîñü, ÷òîáû âñ¸ ýòî ñäåëàòü íàäî áûëî ïðåîäîëåòü — îáîáùèòü, ðàçâèòü òðàäèöèîííîå (ýéëåðîâî) òîëêîâàíèå ôóíêöèè è ïîíÿòèÿ ïðåäåëà.
Èçó÷åíèå ôóíêöèé ïîêàçàëî, ÷òî ôîðìóëà, ïðåäñòàâëÿþùàÿ ôóíêöèþ, è ôóíêöèÿ, åþ ïðåäñòàâëÿåìàÿ — ýòî íå îäíî è òî æå. Ôîðìóëà ÿâëÿåòñÿ îðóäèåì îäíîãî èç ñïîñîáîâ (àíàëèòè÷åñêîãî) ïðåäñòàâëåíèÿ ôóíêöèè. Íàïðèìåð, ôóíêöèÿ f(x)=|x|
ìîæåò áûòü çàäàíà íà ïðîìåæóòêå (–p; +p) äâóìÿ ôîðìóëàìè: ó=õ, ó=–õ
; âìåñòå ñ òåì îíà ìîæåò áûòü çàäàíà è îäíèì àíàëèòè÷åñêèì âûðàæåíèåì, à èìåííî — ñõîäÿùèìñÿ ê íåé òðèãîíîìåòðè÷åñêèì ðÿäîì.
 ïîëüçó ýòîãî çàêëþ÷åíèÿ ãîâîðèëè è èíûå ñîîáðàæåíèÿ. “Íîâåéøèå èññëåäîâàíèÿ ïîêàçàëè,— Ïèñàë Ðèìàí,— ÷òî ñóùåñòâóþò òàêèå àíàëèòè÷åñêèå âûðàæåíèÿ (òðèãîíîìåòðè÷åñêèå ðÿäû), ñ ïîìîùüþ êîòîðûõ ìîæíî â çàäàííîì ïðîìåæóòêå ïðåäñòàâèòü ëþáóþ íåïðåðûâíóþ ôóíêöèþ. Òàêèì îáðàçîì, íå ÿâëÿåòñÿ ñóùåñòâåííûì, áóäåò ëè çàâèñèìîñòü âåëè÷èíû w
îò âåëè÷èíû z
çàäàíà ïðîèçâîëüíî èëè ñ ïîìîùüþ ìàòåìàòè÷åñêîé ôîðìóëû.”
Ïî-íîâîìó áûë ïîñòàâëåí âîïðîñ î íåïðåðûâíîñòè è òî÷êàõ ðàçðûâà ôóíêöèè. Ýéëåðîâî ïîíÿòèå íåïðåðûâíîñòè áûëî îñòàâëåíî, êàê íå îòâå÷àþùåå îáùåìó ïîíÿòèþ ôóíêöèè. Áîëüöàíî, Êîøè, Ëîáà÷åâñêèé, à âñëåä çà íèìè è äðóãèå ìàòåìàòèêè âûäâèãàþò íà ïåðâîå ìåñòî îïðåäåëåíèå íåïðåðûâíîñòè ôóíêöèè “íà ÿçûêå e è d”.
“Ñîãëàñíî ïðàâèëüíîìó îáúÿñíåíèþ,— óêàçûâàë Áîëüöàíî,— ïîíèìàþò ïîä âûðàæåíèåì, ÷òî ôóíêöèÿ f(x)
èçìåíÿåòñÿ ïî çàêîíó íåïðåðûâíîñòè äëÿ âñåõ çíà÷åíèé õ
, êîòîðûå ëåæàò âíóòðè èëè âíå èçâåñòíûõ ãðàíèö; ëèøü òî, ÷òî, åñëè õ
— êàêîå-íèáóäü èç ýòèõ çíà÷åíèé, òîãäà ðàçíîñòü f(x+w)–f(x)
ìîæåò áûòü ñäåëàíà ìåíüøå, ÷åì ëþáàÿ çàäàííàÿ âåëè÷èíà, åñëè ìîæíî ïðèíÿòü w
ñòîëü ìàëûì, ñêîëüêî ìû õîòèì”.
Êîøè ïèñàë: f(x)
íåïðåðûâíà äëÿ çàäàííîãî çíà÷åíèÿ õ
, êîãäà “áåñêîíå÷íî ìàëîå ïðèðàùåíèå ïåðåìåííîé ïðîèçâîäèò áåñêîíå÷íî ìàëûå ïðèðàùåíèÿ ñàìîé ôóíêöèè”.
Ñíà÷àëà òî÷êè ðàçðûâà ôóíêöèè îïðåäåëÿëèñü ÷èñòî îòðèöàòåëüíî. Êîøè ïèñàë: “Êîãäà f(x)
ïåðåñòàåò áûòü íåïðåðûâíî â ñîïðåäåëüíîñòè ÷àñòíîãî çíà÷åíèÿ ïåðåìåííîé õ
, òî ãîâîðÿò, ÷òî îíà äåëàåòñÿ ïðåðûâíîþ
è ÷òî äëÿ ýòîãî ÷àñòíîãî çíà÷åíèÿ ïðîèñõîäèò ðàçðûâ íåïðåðûâíîñòè
”.
Âî âòîðîé ÷åòâåðòè XIX âåêà òî÷êè ðàçðûâà ôóíêöèè f(x)
èçó÷àëè Ïóàññîí, Ëèáðè è äð.  ñâîèõ ìàòåìàòè÷åñêèõ ìåìóàðàõ Ëèáðè ïèñàë, ÷òî âïåðâûå ðàçðûâíûå ôóíêöèè ñäåëàëèñü ïðåäìåòîì èññëåäîâàíèé â ðàáîòàõ Äàíèèëà Áåðíóëëè, Ýéëåðà è Äàëàìáåðà. Îäíàêî, ïîä÷åðêíóë îí, òîëüêî èññëåäîâàíèÿ Ôóðüå, Ïóàññîíà è äðóãèõ ìàòåìàòèêîâ î ðàçðûâíûõ ôóíêöèÿõ ðàññåÿëè âñå ñîìíåíèÿ, êîòîðûå âñå åù¸ ñâÿçûâàëèñü ñ ïðèðîäîé ýòèõ ôóíêöèé. Òî÷íîå ðàçëè÷èå ìåæäó òî÷êàìè ðàçðûâà ïåðâîãî è âòîðîãî ðÿäà è, ñîîòâåòñòâåííî ýòîìó, èõ ïðÿìûå îïðåäåëåíèÿ âîøëè â ïðàêòèêó ìàòåìàòè÷åñêèõ èññëåäîâàíèé âî âòîðîé ïîëîâèíå XIX âåêà.
Íàêîíåö, â ñâÿçè ñî âñåì ýòèì âûÿñíèëîñü, ÷òî íå êàæäàÿ ôóíêöèÿ ÿâëÿåòñÿ âìåñòå ñ òåì è äèôôåðåíöèðóåìîé. Ïåðâûé ïðèìåð íåïðåðûâíîé ôóíêöèè, íå èìåþùåé ïðîèçâîäíîé â êàæäîé òî÷êå, äàë Áîëüöàíî, îäíàêî åãî ïðèìåð â ñâîå âðåìÿ îñòàëñÿ ìàòåìàòèêàì íåèçâåñòíûì.
Âî âòîðîé ïîëîâèíå XIX âåêà ïðèìåð òàêîãî ðîäà ôóíêöèè ïîñòðîèë Áåéåðøòðàññ. Ëîáà÷åâñêèé äàë òî÷íûå îïðåäåëåíèÿ íåïðåðûâíîñòè è äèôôåðåíöèðóåìîñòè ôóíêöèè è ïîä÷åðêíóë ðàçëè÷èÿ ìåæäó ýòèìè ïîíÿòèÿìè.
Òàêèì îáðàçîì, ìîæíî ñêàçàòü, ÷òî â ïåðâîé ÷åòâåðòè XIX âåêà êëàññè÷åñêèé àíàëèç ñòàíîâèòñÿ íàóêîé î âñåõ âîçìîæíûõ âèäàõ ôóíêöèé äåéñòâèòåëüíîãî ïåðåìåííîãî â èõ îáùåì âèäå
. Êîðåííîìó èçìåíåíèþ ïîäâåðãñÿ íå òîëüêî îáúåêò ìàòåìàòè÷åñêîãî àíàëèçà; ïðîèçîøëî êîðåííîå èçìåíåíèå è â ìåòîäàõ
èçó÷åíèÿ ôóíêöèé.
Êàê óæå óêàçûâàëîñü, ðàçâèòèå ïîíÿòèÿ èíòåãðàëà è ðàçðàáîòêà òåõíèêè åãî âû÷èñëåíèÿ ïîêàçàëè, ÷òî îïðåäåëåííûé èíòåãðàë (äâîéíîé, òðîéíîé èíòåãðàëû ïî ïîâåðõíîñòè, íåñîáñòâåííûå èíòåãðàëû) íåîáõîäèìî îáîñíîâûâàòü ñàìîñòîÿòåëüíî, íåçàâèñèìî îò ïîíÿòèÿ íåîïðåäåëåííîãî èíòåãðàëà.  ñâÿçè ñ ýòèì âîçíèê âîïðîñ î ñóùåñòâîâàíèè ïðåäåëîâ èíòåãðàëüíûõ ñóìì, ñëàãàåìûå êîòîðûõ áûëè áû áåñêîíå÷íî ìàëûìè.  ïåðâîé ÷åòâåðòè XIX âåêà ïîíÿòèå áåñêîíå÷íî ìàëîé îêàçàëîñü íåîáõîäèìûì è äëÿ èçó÷åíèÿ è ñîïîñòàâëåíèÿ ñâîéñòâ íåïðåðûâíûõ è ðàçðûâíûõ ôóíêöèé. “Ìåæäó ìíîãèìè ïîíÿòèÿìè,— óêàçûâàë Êîøè,— òåñíî ñâÿçàííûìè ñî ñâîéñòâàìè áåñêîíå÷íî ìàëûõ, ñëåäóåò ïîìåñòèòü ïîíÿòèå î íåïðåðûâíîñòè è ïðåðûâíîñòè ôóíêöèé”. Òóò æå Êîøè äàåò èñòîëêîâàíèå íåïðåðûâíîñòè ôóíêöèè, êîòîðîå áîëåå ÷åì ÿñíî ïîäòâåðæäàåò ÿñíîñòü ýòîãî åãî óòâåðæäåíèÿ.
Íîâàÿ ïîñòàíîâêà çàäà÷ îáîñíîâàíèÿ ìàòåìàòè÷åñêîãî àíàëèçà ÿñíî ïîêàçûâàëà, ÷òî äåëî íå òîëüêî â ïðèçíàíèè è ïðèìåíåíèè áåñêîíå÷íî ìàëûõ — ýòî äåëàëè è ðàíüøå!— íî ïðåæäå âñåãî â íàó÷íîì èñòîëêîâàíèè èõ ñîäåðæàíèÿ è îáîñíîâàííîì íà ýòîì èñïîëüçîâàíèè èõ â àëãîðèòìàõ ìàòåìàòè÷åñêîãî àíàëèçà. Îäíàêî, ÷òîáû ýòî ñäåëàòü íàäî áûëî ïðåîäîëåòü ãîñïîäñòâîâàâøåå â XVIII âåêå óçêîå òîëêîâàíèå ïîíÿòèÿ ïðåäåëà, ðàçðàáîòàòü îáùóþ òåîðèþ ïðåäåëîâ. Ïîëó÷åíèå îñíîâîïîëàãàþùèõ ðåçóëüòàòîâ ñâÿçàíî çäåñü ñ èìåíåì Êîøè.
Èçó÷åíèå ðàçðûâíûõ ôóíêöèé è ñîïîñòàâëåíèå èõ ñ ôóíêöèÿìè íåïðåðûâíûìè çàñòàâèëî ïðèçíàòü òî, ÷òî ðàíåå ñ÷èòàëîñü íåâîçìîæíûì: ÷òî ïðåäåë, ê êîòîðîìó ñòðåìèòüñÿ ïîñëåäîâàòåëüíîñòü çíà÷åíèé ôóíêöèè, ïðè ñòðåìëåíèè àðãóìåíòà â íåêîòîðîé òî÷êå ìîæåò îêàçàòüñÿ îòëè÷íûì îò çíà÷åíèÿ ôóíêöèè â ýòîé òî÷êå
. Çíà÷èò, ïðåäåë íå âñåãäà ÿâëÿåòñÿ “ïîñëåäíèì” çíà÷åíèåì ïåðåìåííîé, íî âî âñåõ ñëó÷àÿõ ïðåäåë åñòü ÷èñëî, ê êîòîðîìó ïåðåìåííàÿ ïðèáëèæàåòñÿ íåîãðàíè÷åííî. Ñëåäîâàòåëüíî, dx
è dy
íå íåîáõîäèìî íóëè èëè ìèñòè÷åñêè àêòóàëüíî áåñêîíå÷íî ìàëûå; áåñêîíå÷íî ìàëàÿ — ýòî ïåðåìåííàÿ, èìåþùàÿ ïðåäåëîì íóëü, ïðè÷åì ôàêò ýòîò ñ ïðîòèâîðå÷èÿìè è ïàðàäîêñàìè íå ñâÿçàí
.
Êîøè ïðåîäîëåë è âòîðóþ îãðàíè÷èòåëüíóþ òåíäåíöèþ â ïðèíÿòîé äî íåãî òðàêòîâêå ïîíÿòèÿ ïðåäåëà. Îí ïðèçíàë, ÷òî ïåðåìåííàÿ ìîæåò ïðèáëèæàòüñÿ ê ñâîåìó ïðåäåëó íå òîëüêî ìîíîòîííî, íî è êîëåáëÿñü, ïîðîé ïðèíèìàÿ çíà÷åíèÿ, ðàâíûå å¸ ïðåäåëó.
Êàê ñïðàâåäëèâî îòìåòèë Í. Í. Ëóçèí, ýòî îáñòîÿòåëüñòâî ïðèäàëî òåîðèè Êîøè íåîáõîäèìóþ îáùíîñòü è èñêëþ÷èòåëüíóþ ãèáêîñòü.
×òî ïîçâîëèëî Êîøè ñäåëàòü ýòî èñêëþ÷èòåëüíî âàæíûé øàã? Îòâåò, êîíå÷íî, íàäî èñêàòü ïðåæäå âñåãî â ñâîåîáðàçèè òåõ ïðåäåëüíûõ ïðîöåññîâ, ñ êîòîðûìè ïðèõîäèëîñü âñòðå÷àòüñÿ â êîíöå XVIII è íà÷àëå XIX âåêà â òî÷íûõ íàóêàõ, îñîáåííî â ìàòåìàòè÷åñêîé ôèçèêå.  ìàòåìàòè÷åñêîì àíàëèçå ê ÷èñëó òàêèõ ïðîöåññîâ íàäî â ïåðâóþ î÷åðåäü îòíåñòè îòûñêàíèå ïðåäåëîâ ðàçëè÷íîãî âèäà èíòåãðàëüíûõ ñóìì è íàõîæäåíèå ñóìì ôóíêöèîíàëüíûõ ðÿäîâ, îñîáåííî òðèãîíîìåòðè÷åñêèõ.
Âûïîëíåííûå Êîøè îáîáùåíèÿ òåîðèè ïðåäåëîâ Íüþòîíà-Äàëàìáåðà ïîçâîëèëè åìó äàòü ïîíÿòèþ áåñêîíå÷íî ìàëîãî ðåàëüíîå èñòîëêîâàíèå è ïîäâåñòè ïîä àëãîðèòì Ëåéáíèöà-Íüþòîíà äîñòàòî÷íûé íàó÷íûé ôóíäàìåíò
. Áëàãîäàðÿ ýòîìó Êîøè ñìîã ïîäâåñòè íàó÷íûé ôóíäàìåíò ïîä ó÷åíèå î íåïðåðûâíîñòè è ðàçðûâàõ ôóíêöèé, îáîñíîâàòü äèôôåðåíöèàëüíîå èñ÷èñëåíèå è, ÷òî îñîáåííî âàæíî, ðàçâèòü íà÷àëà íàó÷íîé êîíöåïöèè îïðåäåëåííîãî èíòåãðàëà.
 ïðîöåññå òàêèõ èññëåäîâàíèé Áîëüöàíî, Êîøè, Ëîáà÷åâñêèé, Äèðèõëå, à âñëåä çà íèìè äðóãèå ïåðåäîâûå ìàòåìàòèêè ïåðâîé ïîëîâèíû XIX âåêà ïî-íîâîìó ïîäîøëè ê èñòîëêîâàíèþ ñòðîãîñòè ìàòåìàòè÷åñêèõ äîêàçàòåëüñòâ, â ïåðâóþ î÷åðåäü äîêàçàòåëüñòâ óòâåðæäåíèé ìàòåìàòè÷åñêîãî àíàëèçà.
Òåîðåìà ñóùåñòâîâàíèÿ (êðèòåðèè ñóùåñòâîâàíèÿ ïðåäåëà ïåðåìåííîé) îêàçàëèñü ñóùåñòâåííî íåîáõîäèìûìè è äëÿ îáîáùåííîé òåîðèè ïðåäåëîâ.
Åñëè ïåðåìåííàÿ èçìåíÿåòñÿ íåïðåðûâíî è ìîíîòîííî, òî ïðèíèìàåìîå åþ ìíîæåñòâî çíà÷åíèé åñòü èíòåðâàë, à ïðåäåë — åãî ïðàâàÿ èëè ëåâàÿ òî÷êà. Êàê ãîâîðèë Í. Í. Ëóçèí, â ýòîì ñëó÷àå ïðåäåë ÿâëÿåòñÿ “îïòè÷åñêèì”: îí âèäåí ãëàçîì. Åñëè æå ñíÿòü ýòè îãðàíè÷åíèÿ, äîïóñòèòü ïðåðûâíîå è, ãëàâíîå, êîëåáëþùååñÿ ïðèáëèæåíèå ïåðåìåííîé ê å¸ ïðåäåëó, òî, âîîáùå ãîâîðÿ, ïðåäåë òåðÿåòñÿ; îí “ãëóáîêî ñïðÿòàí ñðåäè çíà÷åíèé, ïðèíèìàåìûõ ïåðåìåííîé”.  ñâÿçè ñ ýòèì âîçíèêàåò âîïðîñ: ïðè âûïîëíåíèè êàêèõ óñëîâèé ïåðåìåííàÿ èìååò ïðåäåë? Èçâåñòíî, ÷òî è ýòîò âîïðîñ ïîëíîñòüþ ðåøèë Êîøè. Îí äîêàçàë, ÷òî ïîñëåäîâàòåëüíîñòü õ
1
, õ
2
,…, õï
,… èìååò ïðåäåë òîãäà è òîëüêî òîãäà, êîãäà äëÿ âñÿêîãî ïîëîæèòåëüíîãî e, êàê óãîäíî ìàëîãî, ìîæíî íàéòè òàêîå íàòóðàëüíîå ÷èñëî ï
, ÷òî äëÿ ëþáîãî íàòóðàëüíîãî ÷èñëà ò
|xn+m
–xn
|
<e.
Ýòà òåîðåìà â êëàññè÷åñêîì ìàòåìàòè÷åñêîì àíàëèçå èãðàåò ôóíäàìåíòàëüíóþ ðîëü.
Êîãäà ñòàëè ðàçðàáàòûâàòü íîâóþ òåîðèþ ïðåäåëîâ, ïîíÿòèå ðÿäà, ðàíåå íå ðàñ÷ëåíÿåìîå íà ðÿäû ñõîäÿùèåñÿ è íåñõîäÿùèåñÿ, ïîëó÷èëî ïî ýòèì ïðèçíàêàì îñíîâíîå ïîäðàçäåëåíèå. Áëàãîäàðÿ ýòîìó óäàëîñü óñòàíîâèòü òî÷íîå ïîíÿòèå ñóììû ðÿäà è íàïðàâèòü ïî ïðàâèëüíîìó ïóòè ðàçðàáîòêó òåîðèè ÷èñëîâûõ è ñòåïåííûõ ðÿäîâ.  äàëüíåéøåì, â ñâÿçè ñ ðàçðàáîòêîé ïðîáëåì òåîðèè òðèãîíîìåòðè÷åñêèõ ðÿäîâ, áûëî óñòàíîâëåíî, ÷òî ñõîäÿùèåñÿ ÷èñëîâûå ðÿäû ðàñïàäàþòñÿ íà äâà âèäà — àáñîëþòíî è óñëîâíî ñõîäÿùèåñÿ ðÿäû (Äèðèõëå, Ðèìàí). Ïî îñíîâíûì ñâîéñòâàì àáñîëþòíî ñõîäÿùèåñÿ ðÿäû ñõîäíû ñ êîíå÷íûìè ñóììàìè; èõ ìîæíî ïåðåìíîæàòü è ïåðåñòàâëÿòü â íèõ ÷ëåíû. Óñëîâíî ñõîäÿùèåñÿ ðÿäû ñóùåñòâåííî îòëè÷àþòñÿ îò íèõ; Ðèìàí äîêàçàë, ÷òî â ëþáîì, óñëîâíî ñõîäÿùåìñÿ ðÿäå ìîæíî òàê ïåðåñòàâèòü åãî ÷ëåíû, ÷òî âíîâü ïîëó÷åííûé ðÿä áóäåò èìåòü ñóììîé íàïåðåä çàäàííîå ÷èñëî; ìîæíî òàêæå äîáèòüñÿ òîãî, ÷òîáû íîâûé ðÿä îêàçàëñÿ ðàñõîäÿùèìñÿ. Ñëåäîâàòåëüíî, àëãîðèòìû, îñíîâàííûå íà ñâîéñòâå êîíå÷íûõ ñóìì, ìîæíî îòíîñèòü òîëüêî ê àáñîëþòíî ñõîäÿùèìñÿ ðÿäàì. Ê ïåðâîé ÷åòâåðòè XIX âåêà îòíîñèòñÿ îòêðûòèå Êîøè ôóíêöèè  , äëÿ êîòîðîé ìîæíî ñîñòàâèòü ðÿä Ìàêëîðåíà, ñõîäÿùèéñÿ ïðè âñÿêîì õ
, íî êîòîðûé ñõîäèòñÿ âñþäó ê íóëþ, à íå ê ýòîé ôóíêöèè. , äëÿ êîòîðîé ìîæíî ñîñòàâèòü ðÿä Ìàêëîðåíà, ñõîäÿùèéñÿ ïðè âñÿêîì õ
, íî êîòîðûé ñõîäèòñÿ âñþäó ê íóëþ, à íå ê ýòîé ôóíêöèè.
Òåì ñàìûì áûëà äîêàçàíà îøèáî÷íîñòü èñõîäíîãî ïîëîæåíèÿ Ëàãðàíæà, ñäåëàííîãî èì ïðè ïîïûòêå îáîñíîâàòü äèôôåðåíöèàëüíîå èñ÷èñëåíèå íà áàçå òåîðèè ñòåïåííûõ ðÿäîâ. Îñîáóþ ðîëü ñûãðàëè èññëåäîâàíèÿ ïî òðèãîíîìåòðè÷åñêèì ðÿäàì (Äèðèõëå, Ðèìàí, Ëîáà÷åâñêèé è äð.). Áëàãîäàðÿ èì íà÷àëà ñîçäàâàòüñÿ îáùàÿ òåîðèÿ ôóíêöèîíàëüíûõ ðÿäîâ, âêëþ÷èâøàÿ òåîðèþ ñòåïåííûõ ðÿäîâ êàê ÷àñòíûé ñëó÷àé.
Òàêîãî ðîäà ôàêòû çàñòàâèëè ìàòåìàòèêîâ îòêàçàòüñÿ îò íåîáîñíîâàííîãî, ÷àñòî ôîðìàëüíîãî ïåðåíåñåíèÿ îñíîâíûõ ïîíÿòèé è ñâîéñòâ êîíå÷íûõ ñóìì íà âñå áåñêîíå÷íûå ðÿäû è ïîìîãëè èì ðàçðàáîòàòü íàó÷íûå ïðèíöèïû òåîðèè ðÿäîâ, áàçèðóþùèåñÿ íà òåîðèè ïðåäåëîâ.
Ýòè æå ôàêòû ïîìîãëè ìàòåìàòèêàì ïåðâîé ïîëîâèíû XIX âåêà ïîíÿòü, ïî÷åìó ìàòåìàòèêè XVIII âåêà íå ñìîãëè ñäåëàòü â òåîðèè ðÿäîâ òî, ÷òî óäàëîñü ñäåëàòü èì. Òàê, ñîïîñòàâèâ ñâîéñòâà àáñîëþòíî è óñëîâíî ñõîäÿùèõñÿ ðÿäîâ, Ðèìàí çàìåòèë:
“Òîëüêî ê ðÿäàì ïåðâîãî êëàññà ïðèìåíèìû çàêîíû êîíå÷íûõ ñóìì; òîëüêî ýòè ðÿäû ìîãóò áûòü â ïîäëèííîì ñìûñëå ðàññìàòðèâàåìû êàê ñóììà âñåõ ñâîèõ ÷ëåíîâ; î ðÿäàõ æå âòîðîãî êëàññà òîãî æå ñêàçàòü íåëüçÿ,— îáñòîÿòåëüñòâî, óïóùåííîå èç âèäà ìàòåìàòèêàìè ïðîøëîãî ñòîëåòèÿ, âåðîÿòíî, ïî òîé ïðè÷èíå, ÷òî ðÿäû, ðàñïîëîæåííûå ïî âîçðàñòàþùèì ñòåïåíÿì ïåðåìåííîé, âîîáùå ãîâîðÿ (ò. å. äëÿ âñåõ çíà÷åíèé ïåðåìåííîé, êðîìå íåêîòîðûõ îòäåëüíûõ), ïðèíàäëåæàò ê ïåðâîìó êëàññó.”
Îïèñàííûé âûøå ïðîöåññ èçìåíåíèÿ ñîäåðæàíèÿ è êîðåííîãî ïðåîáðàçîâàíèÿ ìåòîäîëîãèè ìàòåìàòè÷åñêîãî àíàëèçà è òåîðèè ðÿäîâ â îáùèõ ÷åðòàõ áûë ïðèñóù áîëüøèíñòâó ìàòåìàòè÷åñêèõ äèñöèïëèí ïåðâîé ïîëîâèíû XIX âåêà.  ñâÿçè ñ ýòèì ñ ïåðâîé ïîëîâèíû XIX âåêà ñîçäàåòñÿ, à âî âòîðîé ïîëó÷àåò âñåîáùåå ïðèçíàíèå íîâûé èäåàë ñòðîãîãî îáîñíîâàíèÿ ìàòåìàòè÷åñêîé òåîðèè, ñâîäÿùèéñÿ ê òðåì òðåáîâàíèÿì:
íå ñ÷èòàòü íåâîçìîæíûì òî, ÷òî êàæåòñÿ ïàðàäîêñàëüíûì.
Ãàóññ ïèñàë: “Ìû íå ìîæåì ñìåøèâàòü òî, ÷òî íàì êàæåòñÿ íååñòåñòâåííûì, ñ òåì, ÷òî íàì êàæåòñÿ àáñîëþòíî íåâîçìîæíûì”.
èçó÷àòü âñå âîçìîæíîñòè, êàêèå ïðåäñòàâëÿåò ïðåäìåò èññëåäîâàíèÿ è ñîîòâåòñòâåííî ýòîìó ðàçâèâàòü îáùèå òåîðèè.
 ïåðâîé ïîëîâèíå XIX âåêà ýòîò ïðèíöèï ñòàíîâèòñÿ ðóêîâîäÿùèì íà÷àëîì èññëåäîâàíèé ïî÷òè âñåõ âåäóùèõ ìàòåìàòèêîâ.
ïðåæäå ÷åì çàäàâàòüñÿ âîïðîñîì î çàâèñèìîñòè, ñóùåñòâîâàíèå êîòîðîé îñòà¸òñÿ íåèçâåñòíûì, ñëåäóåò ïîñòàâèòü âîïðîñ, âîçìîæíà ëè â äåéñòâèòåëüíîñòè òàêàÿ çàâèñèìîñòü.
(Àáåëü)
Âî âòîðîé ÷åòâåðòè XIX âåêà îáû÷íûå êîìïëåêñíûå ÷èñëà íàøëè øèðîêîå ïðèìåíåíèå â òåîðèè ôóíêöèé è äàæå â òåîðèè ÷èñåë.  òîæå âðåìÿ ðàçðàáîòêà ïðîáëåì ï
-ìåðíîé ãåîìåòðèè è ìåòîäîâ ìàòåìàòè÷åñêîé ôèçèêè ïîòðåáîâàëà äàëüíåéøåãî îáîáùåíèÿ ïîíÿòèÿ ÷èñëà, ïåðåõîäà ê íîâîãî âèäà êîìïëåêñíûì ÷èñëàì ñ ï
îñíîâíûìè åäèíèöàìè. Êîìïëåêñíûå è ãèïåðêîìïëåêñíûå ÷èñëà ñòàëè ïðåäñòàâèòåëÿìè èññëåäóåìûõ ðåàëüíûõ âåëè÷èí — âåêòîðîâ â ïðîñòðàíñòâå Rn
; îòâåò íà çàäà÷ó, âûðàæåííûé êîìïëåêñíûì èëè ãèïåðêîìïëåêñíûì ÷èñëîì, èìåë â ýòîé îáëàñòè îáúåêòèâíûé ñìûñë. Îáúÿâëÿòü êîìïëåêñíûå (è ãèïåðêîìïëåêñíûå) ÷èñëà “ëîæíûìè”, “âîîáðàæàåìûìè”, “ìíèìûìè”, êàê ýòî äåëàëè ìàòåìàòèêè XVII–XVIII âåêîâ, ñòàëî íåâîçìîæíûì.
Àðèôìåòèêà êîìïëåêñíûõ è ãèïåðêîìïëåêñíûõ ÷èñåë ïîêàçàëà äàëåå, ÷òî ïåðåõîä ê íîâîé, áîëåå øèðîêîé îáëàñòè ÷èñåë ñâÿçàí, âî-ïåðâûõ, ñ íåîáõîäèìîñòüþ îáîáùàòü îïðåäåëåíèÿ äåéñòâèé, äàííûõ äëÿ èñõîäíîé îáëàñòè ÷èñåë è, âî-âòîðûõ, ñîïðîâîæäàåòñÿ ïîòåðåé íåêîòîðûõ ñâîéñòâ, ïðèñóùèõ ÷èñëàì èñõîäíîé îáëàñòè ÷èñåë. Ïðè ïåðåõîäå îò äåéñòâèòåëüíûõ ê êîìïëåêñíûì ÷èñëàì ïðèøëîñü îòêàçàòüñÿ îò ñâÿçûâàíèÿ èõ çíàêàìè >, <.  àðèôìåòèêå êâàòåðíèîíîâ ñòàëî íåîáõîäèìûì äîïîëíèòåëüíî îòêàçàòüñÿ è îò çàêîíà ïåðåìåñòèòåëüíîñòè óìíîæåíèÿ. Çàêîíû ñ÷åòà — èñòîðè÷åñêè ñàìûå ñòîéêèå, à ïîýòîìó â ïîíèìàíèè ìàòåìàòèêîâ XVII–XVIII âåêîâ ñîñòàâëÿþùèå îñíîâó “íåèçìåííîé ñóùíîñòè” ïîíÿòèÿ ÷èñëà îêàçàëèñü çàêîíàìè ñ îãðàíè÷åííîé îáëàñòüþ äåéñòâèÿ
.
Ìåòàôèçè÷åñêîå ðàçäåëåíèå ÷èñåë íà “ðåàëüíûå” è “âîîáðàæàåìûå”, òðåáîâàíèå ñòðîèòü ó÷åíèå î ÷èñëàõ íà îáû÷íûõ îïðåäåëåíèÿõ àðèôìåòè÷åñêèõ äåéñòâèé, ÷èñòî ôîðìàëüíîå ïîäâåäåíèå íîâûõ ÷èñåë ïîä âñå çàêîíû ÷èñåë èçâåñòíûõ — âñå ýòî îêàçàëîñü îêîí÷àòåëüíî äèñêðåäèòèðîâàííûì.
Ýòè ôàêòû (ñ ó÷åòîì îáùèõ òåíäåíöèé ðàçâèòèÿ ñïîñîáîâ îáîñíîâàíèÿ ìàòåìàòèêè) ïîêàçàëè, ÷òî äëÿ îáîñíîâàíèÿ àðèôìåòèêè êàêîãî óãîäíî âèäà ÷èñåë, îáúåêòèâíîñòü êîòîðûõ óæå äîêàçàíà, äîñòàòî÷íî ïåðå÷èñëèòü å¸ îñíîâíûå ïîíÿòèÿ, îïðåäåëåíèÿ è ïîñûëêè, âûÿñíèòü, êàêèå çàêîíû ñ÷åòà âûïîëíÿþòñÿ â îáîñíîâûâàåìîé îáëàñòè ÷èñåë, à âñå îñòàëüíûå å¸ óòâåðæäåíèÿ ïîëó÷èòü â ðåçóëüòàòå äåäóêöèé. Íà ýòîì ïóòè óäàëîñü îáîñíîâàòü àðèôìåòèêè öåëûõ, ðàöèîíàëüíûõ, êîìïëåêñíûõ è ãèïåðêîìïëåêñíûõ ÷èñåë. Àðèôìåòèêà íàòóðàëüíûõ è àðèôìåòèêà äåéñòâèòåëüíûõ ÷èñåë ïîëó÷èëà ðåàëüíîå îáîñíîâàíèå âî âòîðîé ïîëîâèíå XIX âåêà.
 òåñíîé ñâÿçè ñ îáîáùåíèåì ïîíÿòèÿ ÷èñëà è ñ íîâûìè ñïîñîáàìè îáîñíîâàíèÿ ó÷åíèÿ î ÷èñëå íàõîäèòñÿ âîçíèêíîâåíèå èñõîäíûõ èäåé “ôîðìàëüíîé” àëãåáðû. Ýòèìè èäåÿìè ìàòåìàòèêà îáÿçàíà Ïèêîêó, Ãàìèëüòîíó, À. äå Ìîðãàíó, Ãðåãîðè è Ãàíêåëþ.
 ãåîìåòðèè áûëè ñäåëàíû îòêðûòèÿ, èìåþùèå äëÿ å¸ îñíîâàíèé ôóíäàìåíòàëüíîå çíà÷åíèå.
Ëîáà÷åâñêèé è Áîéëè îòêðûëè íååâêëèäîâó ãåîìåòðèþ. Ïîíñåëå ðàçðàáîòàë ïðîåêòèâíóþ ãåîìåòðèþ, Ãðàññìàí — ãåîìåòðèþ ï
-ìåðíûõ ïðîñòðàíñòâ. Ïðèíöèïû ýòèõ ãåîìåòðè÷åñêèõ òåîðèé ñóùåñòâåííî îòëè÷àþòñÿ îò ïîñûëîê “Íà÷àë” Åâêëèäà.
Îäíàêî, â ïåðâîé ïîëîâèíå XIX âåêà íååâêëèäîâà ãåîìåòðèÿ ïðèçíàíèÿ íå ïîëó÷èëà. Ïðîåêòèâíàÿ ãåîìåòðèÿ áûëà ðàçðàáîòàíà Ïîíñåëå êàê íàäñòðîéêà íàä ãåîìåòðèåé Åâêëèäà; å¸ áîëåå îáùåå ñîäåðæàíèå è ñïåöèôèêà å¸ ïðèíöèïîâ áûëè îñîçíàíû âî âòîðîé ïîëîâèíå XIX âåêà. Ã. Ãðàññìàí ðàçâèë ñâîå ó÷åíèå íà ðóáåæå ñåðåäèíû XIX âåêà. Áëàãîäàðÿ ýòîìó óêàçàííûå âûâîäû ïîëó÷èëè âïîñëåäñòâèè øèðîêîå ïðèçíàíèå.
Âîò åù¸ îäèí ðåçóëüòàò, èìåþùèé ôóíäàìåíòàëüíîå çíà÷åíèå äëÿ îáîñíîâàíèÿ ìàòåìàòèêè. Ìàòåìàòèêè XVII–XVIII âåêîâ ïûòàëèñü äîêàçàòü, ÷òî âñÿêîå óðàâíåíèå ïÿòîé ñòåïåíè ðàçðåøèìî â ðàäèêàëàõ.  1827 ãîäó Àáåëü äîêàçàë, ÷òî ýòî íåâîçìîæíî. Ïîñêîëüêó âñå æå ñóùåñòâóþò óðàâíåíèÿ ïÿòîé, øåñòîé è äðóãèõ ñòåïåíåé, ðàçðåøàåìûå â ðàäèêàëàõ, åñòåñòâåííî âîçíèêàë âîïðîñ: êàê îõàðàêòåðèçîâàòü êëàññ óðàâíåíèé äàííîé ñòåïåíè, êîòîðûå äîïóñêàþò ðåøåíèå â ðàäèêàëàõ? Ýòîò âîïðîñ èìåë è ïðàêòè÷åñêîå çíà÷åíèå. Êàê ïîêàçàëè Ýéëåð è Äàëàìáåð, èíòåãðèðîâàíèå ëèíåéíûõ äèôôåðåíöèàëüíûõ óðàâíåíèé ï
-ãîïîðÿäêà ñ ïîñòîÿííûìè êîýôôèöèåíòàìè ñâîäèòñÿ ê íàõîæäåíèþ êîðíåé àëãåáðàè÷åñêîãî óðàâíåíèÿ ï
-é ñòåïåíè. Òàêèå äèôôåðåíöèàëüíûå óðàâíåíèÿ ÿâëÿþòñÿ ìàòåìàòè÷åñêèì àïïàðàòîì òåîðèè êîëåáàíèé. ×òîáû ðåøèòü óêàçàííûé âûøå âîïðîñ, Ý. Ãàëóà ïîñòðîèë îñîáûé ìàòåìàòè÷åñêèé àïïàðàò, â êîòîðîì ãëàâíàÿ ðîëü îòâîäèòñÿ ïîíÿòèþ ãðóïïû. Âûÿñíèëîñü, ÷òî ïîä ïîíÿòèå ãðóïïû ïîäõîäÿò ðàçëè÷íûå îáëàñòè îáúåêòîâ, áëàãîäàðÿ ÷åìó îíî íàõîäèò ïëîäîòâîðíîå ïðèìåíåíèå â ðàçëè÷íûõ ìàòåìàòè÷åñêèõ äèñöèïëèíàõ. Îêàçàëîñü òàêæå, ÷òî ïîíÿòèå ãðóïïû îáíàðóæèâàåò ñâîþ äåéñòâåííîñòü íàèëó÷øèì îáðàçîì, êîãäà åãî òåîðèÿ îáîñíîâûâàåòñÿ àáñòðàêòíî, íåçàâèñèìî îò îïèñàíèÿ ïðèðîäû îáúåêòîâ, îòíîøåíèÿ êîòîðûõ åþ îïèñûâàþòñÿ. Âïåðâûå âñå ýòè ôàêòû îò÷åòëèâî îñîçíàë è îïèñàë Êýëè â 1854 ãîäó; ýòîò ãîä ïîýòîìó ñ÷èòàþò ãîäîì íà÷àëà àáñòðàêòíîé òåîðèè ãðóïï.
Ïîä âëèÿíèåì âñåõ ýòèõ ôàêòîâ â ïåðâîé ïîëîâèíå XIX âåêà ïðåäïðèíèìàþòñÿ ïîïûòêè ðàñøèðèòü òðàäèöèîííîå îïðåäåëåíèå ïðåäìåòà ìàòåìàòèêè êàê íàóêè òîëüêî î âåëè÷èíàõ è èõ èçìåðåíèè. Íàïðèìåð, äëÿ Ïóàíñî ìàòåìàòèêà — ýòî íàóêà î ñâîéñòâàõ ÷èñåë, âåëè÷èíàõ è ïîðÿäêå. Áîëüöàíî è Ãðàññìàí ñ÷èòàëè, ÷òî òðàäèöèîííàÿ òðàêòîâêà î ïðåäìåòå ìàòåìàòèêè íå îõâàòûâàåò å¸ ñîäåðæàíèÿ â öåëîì: íàïðèìåð, îíî íå ïðèëîæèìî ê ó÷åíèþ î ñî÷åòàíèÿõ. Äëÿ Ãðàññìàíà ìàòåìàòèêà — ó÷åíèå î ôîðìàõ, îäíàêî ãåîìåòðèÿ ê ìàòåìàòèêå íå ïðèíàäëåæèò.  1854 ãîäó Äæ. Áóëü ïîä÷åðêèâàë, ÷òî “â ïðèðîäå ìàòåìàòèêè íå çàëîæåíà íåîáõîäèìîñòü çàíèìàòüñÿ èäåÿìè ÷èñëà è âåëè÷èíû”.
Èòàê, ðàçðàáîòàííûå â ïåðâîé ïîëîâèíå XIX âåêà ñïîñîáû îáîñíîâàíèÿ è ìåòîäû ìàòåìàòèêè ïîçâîëèëè ìàòåìàòèêàì ïåðåñòðîèòü ìàòåìàòè÷åñêèé àíàëèç, àëãåáðó, ó÷åíèå î ÷èñëå è îò÷àñòè ãåîìåòðèþ â ñîîòâåòñòâèè ñ òðåáîâàíèÿìè íîâîé ìåòîäîëîãèè. Íîâàÿ ìåòîäîëîãèÿ ìàòåìàòèêè ñïîñîáñòâîâàëà ïðåîäîëåíèþ êðèçèñà å¸ îñíîâ è ñîçäàëà äëÿ íå¸ øèðîêèå ïåðñïåêòèâû äàëüíåéøåãî ðàçâèòèÿ.
Äëÿ ÷åãî ìàòåìàòèêè ïîñëåäíèõ äåñÿòèëåòèé XIX âåêà ïîòðåáîâàëîñü îáùåå ó÷åíèå î ìíîæåñòâàõ, îðãàíè÷åñêè ñâÿçàííûõ ñ ïîíÿòèåì àêòóàëüíîé áåñêîíå÷íîñòè? Ã. Êàíòîð îòâåòèë íà ýòîò âîïðîñ òàê: “…äëÿ îáîñíîâàíèÿ àðèôìåòèêè äåéñòâèòåëüíûõ ÷èñåë, äëÿ äîêàçàòåëüñòâà ôóíäàìåíòàëüíûõ òåîðåì ìàòåìàòè÷åñêîãî àíàëèçà è òåîðèè òðèãîíîìåòðè÷åñêèõ ðÿäîâ”. Ã. Êàíòîð óêàçûâàë òàêæå, ÷òî èäåè è ìåòîäû îáùåãî ó÷åíèÿ î ìíîæåñòâàõ ÿâëÿþòñÿ äåéñòâåííûìè îðóäèÿìè îòûñêàíèÿ íîâûõ ìàòåìàòè÷åñêèõ ôàêòîâ è ðàçâèòèÿ íîâûõ ìàòåìàòè÷åñêèõ òåîðèé.  ýòîé ñâÿçè îí ñ÷åë âîçìîæíûì óòâåðæäàòü, ÷òî äëÿ ìàòåìàòèêè ïîíÿòèå àêòóàëüíîé áåñêîíå÷íîñòè ñóùåñòâåííî íåîáõîäèìî.
Îñíîâíûì ïîíÿòèåì îáùåãî ó÷åíèÿ î ìíîæåñòâàõ Ã. Êàíòîðà ÿâëÿåòñÿ ïîíÿòèå áåñêîíå÷íîãî ìíîæåñòâà
(ïîíÿòèå àêòóàëüíîé áåñêîíå÷íîñòè
). “Ïîä ìíîãîîáðàçèåì, èëè ìíîæåñòâîì,— ïèñàë Ã. Êàíòîð,— ÿ ïîíèìàþ âîîáùå âñÿêîå ìíîãîå, êîòîðîå ìîæíî ìûñëèòü êàê åäèíîå, ò. å. âñÿêóþ ñîâîêóïíîñòü îïðåäåëåííûõ ýëåìåíòîâ, êîòîðàÿ ìîæåò áûòü ñâÿçàíà â îäíî öåëîå ñ ïîìîùüþ íåêîòîðîãî çàêîíà.”
Êàíòîð íàçûâàë ìíîæåñòâî Ð
îïðåäåëåííûì, åñëè îòíîñèòåëüíî ëþáîãî îáúåêòà ìîæíî ñêàçàòü, ïðèíàäëåæèò îí ìíîæåñòâó Ð
èëè íå ïðèíàäëåæèò.
Ïîíÿòèå çàêîíà Ã. Êàíòîð ñ÷èòàë èñõîäíûì, íåîïðåäåëèìûì. Âìåñòå ñ òåì, â åãî êîíöåïöèè ïîíÿòèå çàêîíà èãðàåò ôóíäàìåíòàëüíóþ ðîëü. Òàê êàê ñîãëàñíî çàêîíó ýëåìåíòû íåêîòîðîé ñîâîêóïíîñòè ìîãóò áûòü ñâÿçàíû â îäíî öåëîå, òî çàêîí îáåñïå÷èâàåò ñóùåñòâîâàíèå ìíîæåñòâà. Âåðíî è îáðàòíîå: åñëè ìíîæåñòâî ñóùåñòâóåò, òî ìîæíî äàòü çàêîí, îáåñïå÷èâàþùèé åãî ñóùåñòâîâàíèå.
Îïåðàòèâíûìè ïîíÿòèÿìè îáùåãî ó÷åíèÿ î ìíîæåñòâàõ Ã. Êàíòîðà ÿâëÿþòñÿ ïîíÿòèÿ âçàèìíî îäíîçíà÷íîãî ñîîòâåòñòâèÿ ìîùíîñòè è êîëè÷åñòâà ìíîæåñòâà.
Êàíòîð îïðåäåëèë ìîùíîñòü — òåïåðü ÷àñòî ãîâîðÿò: “êîëè÷åñòâåííîå ÷èñëî” — êàê ðåçóëüòàò àáñòðàêöèè îò ñîäåðæàíèÿ è ïîðÿäêà ýëåìåíòîâ ìíîæåñòâà.
Îí íàçûâàë äâà ìíîæåñòâà ðàâíîìîùíûìè è èìåþùèìè îäèíàêîâóþ ìîùíîñòü, åñëè ìåæäó èõ ýëåìåíòàìè âîçìîæíî óñòàíîâèòü âçàèìíî îäíîçíà÷íîå ñîîòâåòñòâèå.
Äëÿ ðàçâèòèÿ îáùåãî ó÷åíèÿ î ìíîæåñòâàõ íàèáîëåå ñóùåñòâåííûì ÿâèëîñü äðóãîå îòêðûòèå Ã. Êàíòîðà — äîêàçàòåëüñòâî ñóùåñòâîâàíèÿ áåñêîíå÷íûõ ìíîæåñòâ ñ ðàçëè÷íûìè ìîùíîñòÿìè.
Åñëè ìíîæåñòâî êîíå÷íî, ïîíÿòèå ìîùíîñòè ñîâïàäàåò ñ ïîíÿòèåì ÷èñëà åãî ýëåìåíòîâ è ìîæåò áûòü âûðàæåíî êîëè÷åñòâåííûì íàòóðàëüíûì ÷èñëîì.  ñëó÷àÿõ áåñêîíå÷íûõ ìíîæåñòâ íåëüçÿ ãîâîðèòü î ÷èñëå èõ ýëåìåíòîâ, íî êàæäîìó èç òàêèõ ìíîæåñòâ ìîæíî ïðèïèñàòü îïðåäåëåííóþ ìîùíîñòü. Ïðèíÿòî îòíîñèòü êàæäîìó êëàññó ìíîæåñòâ íåêîòîðûé ñèìâîë ìîùíîñòè. Òàê  — ñèìâîë ìîùíîñòè ñ÷åòíîãî ìíîæåñòâà, ñ
— ñèìâîë ìîùíîñòè êîíòèíóóìà, 2ò
— ñèìâîë ìîùíîñòè ìíîæåñòâà âñåõ ïîäìíîæåñòâ ìíîæåñòâà, ìîùíîñòü êîòîðîãî åñòü ò
. Êàæäûé òàêîé ñèìâîë Êàíòîð íàçâàë êàðäèíàëüíûì òðàíñôèíèòíûì
÷èñëîì. — ñèìâîë ìîùíîñòè ñ÷åòíîãî ìíîæåñòâà, ñ
— ñèìâîë ìîùíîñòè êîíòèíóóìà, 2ò
— ñèìâîë ìîùíîñòè ìíîæåñòâà âñåõ ïîäìíîæåñòâ ìíîæåñòâà, ìîùíîñòü êîòîðîãî åñòü ò
. Êàæäûé òàêîé ñèìâîë Êàíòîð íàçâàë êàðäèíàëüíûì òðàíñôèíèòíûì
÷èñëîì.
Êàíòîð ïðåäïðèíÿë ïîïûòêó ðàçâèòü àðèôìåòèêó êàðäèíàëüíûõ òðàíñôèíèòíûõ ÷èñåë. Îí äîêàçàë ìíîãèå àðèôìåòè÷åñêèå ñîîòíîøåíèÿ, ñïðàâåäëèâûå äëÿ ìîùíîñòåé êîíêðåòíûõ ìíîæåñòâ — ñ÷åòíûõ è ìîùíîñòè êîíòèíóóìà. Íàïðèìåð, åñëè ï
— ëþáîå íàòóðàëüíîå ÷èñëî, òî:
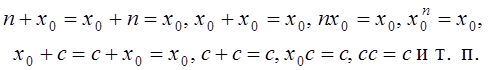
Íî êîãäà êàíòîð ïîïûòàëñÿ îáîáùèòü ïîëó÷åííûå èì àðèôìåòè÷åñêèå ñîîòíîøåíèÿ íà ëþáûå êàðäèíàëüíûå òðàíñôèíèòíûå ÷èñëà, òî âñòðåòèëñÿ ñ ñåðüåçíûìè òðóäíîñòÿìè.
Ïóñòü Ì
è N
— êàêèå óãîäíî áåñêîíå÷íûå ìíîæåñòâà, ò
è ï
— ñîîòâåòñòâóþùèå èì êàðäèíàëüíûå òðàíñôèíèòíûå ÷èñëà. Ìîæíî ëè óòâåðæäàòü, ÷òî ýòè ÷èñëà âñåãäà ìîãóò áûòü ñâÿçàíû îäíèì è òîëüêî îäíèì èç çíàêîâ =, >, <? Äëÿ íàòóðàëüíûõ ÷èñåë ò
è ï
ýòî óòâåðæäåíèå ñïðàâåäëèâî, äëÿ êàðäèíàëüíûõ òðàíñôèíèòíûõ ÷èñåë ñïðàâåäëèâîñòü åãî íå î÷åâèäíà. Êàíòîð ýòó ïðîáëåìó íå ðåøèë, å¸ íàçâàëè ïðîáëåìîé òðèõîòîìèè
. Êàíòîð íå ñìîã òàêæå äîêàçàòü (èëè îïðîâåðãíóòü), ÷òî äëÿ ëþáûõ êàðäèíàëüíûõ òðàíñôèíèòíûõ ÷èñåë ñïðàâåäëèâû ñîîòíîøåíèÿ:
ò+ï=òï
;
ò=ò
2
;
åñëè ò
2
=ï
2
, òî ò=ï
;
åñëè ò<ï
è p<q
, òî m+p<n+q
;
åñëè ò<ï
è p<q
, òî mp<nq
.
À. Òàðñêèé äîêàçàë, ÷òî êàæäîå èç ýòèõ ñîîòíîøåíèé ýêâèâàëåíòíî òðèõîòîìèè.
Èçâåñòíî, ÷òî x0
<c
. Ñóùåñòâóåò ëè ìíîæåñòâî Ì
, ìîùíîñòü êîòîðîãî ò
óäîâëåòâîðÿåò íåðàâåíñòâàì:
õ0
<m<c
?
Ýòó ïðîáëåìó Êàíòîð òàêæå íå ðåøèë. Îí âûñêàçàë ïðåäïîëîæåíèå, ÷òî òàêîå ìíîæåñòâî Ì
íå ñóùåñòâóåò. Ïðåäïîëîæåíèå Êàíòîðà íàçûâàëîñü ãèïîòåçîé êîíòèíóóìà
; îíî ýêâèâàëåíòíî óòâåðæäåíèþ, ÷òî âñÿêîå íå÷åòíîå ìíîæåñòâî äåéñòâèòåëüíûõ ÷èñåë èìååò ìîùíîñòü êîíòèíóóìà
.
Ïîñëå ïóáëèêàöèè ïåðâûõ ðàáîò Ã. Êàíòîðà, â êîòîðûõ îí èçëîæèë íà÷àëà ó÷åíèÿ î òðàíñôèíèòíûõ ÷èñëàõ (êîëè÷åñòâåííûõ è ïîðÿäêîâûõ), ìàòåìàòèêè, ëîãèêè, ôèëîñîôû è îñîáåííî òåîëîãè îòíåñëèñü ê åãî èäåÿì âåñüìà ñäåðæàííî. Íåêîòîðûå èç íèõ âûñòóïèëè ñ îòêðûòîé êðèòèêîé îñíîâíîãî ïîíÿòèÿ ó÷åíèÿ Êàíòîðà — ïîíÿòèÿ àêòóàëüíîé áåñêîíå÷íîñòè. Êàíòîð îòâåòèë íà ýòè âûñòóïëåíèÿ â íåñêîëüêèõ ñòàòüÿõ è â ïåðåïèñêå, êîòîðóþ âïîñëåäñòâèè ÷àñòè÷íî îïóáëèêîâàë.
Íàèáîëåå ñåðüåçíûì ïðîòèâíèêîì êîíöåïöèè Êàíòîðà áûë Ë. Êðîíåêåð. Îí ñ÷èòàë, ÷òî äåéñòâèòåëüíî ñóùåñòâóþùèìè, ðåàëüíûìè ìîæíî ïðèçíàòü ëèøü íàòóðàëüíûå ÷èñëà, âñëåäñòâèå ÷åãî îíè ÿâëÿþòñÿ åäèíñòâåííûì îáúåêòîì ÷èñòîé ìàòåìàòèêè. Êðîíåêåð óòâåðæäàë, ÷òî âñå òåîðåìû ìàòåìàòè÷åñêîãî àíàëèçà ïðàâîìåðíû ëèøü ïîñòîëüêó, ïîñêîëüêó èõ ìîæíî èñòîëêîâàòü êàê îïèñàíèÿ çàêîíîâ, ãîñïîäñòâóþùèõ â îáëàñòè íàòóðàëüíûõ ÷èñåë. Ñ ýòîé òî÷êè çðåíèÿ, ïèñàë Êàíòîð, èçâåñòíàÿ ðåàëüíîñòü ïðèïèñûâàåòñÿ òàêæå ðàöèîíàëüíûì ÷èñëàì, ïîñêîëüêó îíè “íåïîñðåäñòâåííî âûòåêàþò” èç àðèôìåòèêè íàòóðàëüíûõ ÷èñåë. Êðîíåêåð òðàêòîâàë èððàöèîíàëüíûå ÷èñëà êàê óäîáíûå ñèìâîëû äëÿ îïèñàíèÿ åäèíûì ñïîñîáîì ñâîéñòâ ãðóïï íàòóðàëüíûõ ÷èñåë; ïîíÿòèå àêòóàëüíîé áåñêîíå÷íîñòè îí ïîëíîñòüþ îòðèöàë. Ñëåäóÿ ýòèì èäåÿì, Êðîíåêåð îïóáëèêîâàë èññëåäîâàíèå, â êîòîðîì íàìåòèë êîíòóðû íåêîòîðûõ “âñïîìîãàòåëüíûõ òåîðèé”, ïî åãî ìíåíèþ ïîçâîëÿþùèõ îñâîáîäèòü ÷èñòóþ ìàòåìàòèêó îò èððàöèîíàëüíûõ ÷èñåë.
Êàíòîð îòìå÷àë, ÷òî êîíöåïöèÿ Êðîíåêåðà, â ñðàâíåíèè ñ îáùåïðèçíàííûìè òåîðèÿìè ÷èñòîé ìàòåìàòèêè, îáëàäàåò íåêîòîðûìè ïðåèìóùåñòâàìè. Åñëè ñòðîãî ïðèäåðæèâàòüñÿ êîíöåïöèè Êðîíåêåðà, òî “âîçìîæíî ïîòðåáîâàòü”, ÷òîáû äîêàçàòåëüñòâà àíàëèòè÷åñêèõ òåîðåì áûëè èñïûòàíû ïî ñâîåìó “òåîðåòèêî-÷èñëîâîìó ñîäåðæàíèþ” è ÷òîáû êàæäûé îáíàðóæèâàþùèéñÿ â íèõ ïðîáåë áûë çàïîëíåí ñîãëàñíî ïðèíöèïàì àðèôìåòèêè.  âîçìîæíîñòè ïîäîáíîãî äîïîëíåíèÿ çàêëþ÷àåòñÿ íàñòîÿùèé ïðîáíûé êàìåíü äëÿ ïðàâèëüíîñòè è ïîëíîé ñòðîãîñòè äîêàçàòåëüñòâ. Òàêèå äîïîëíåíèÿ ñïîñîáíû ïðåäîõðàíèòü èññëåäîâàòåëåé îò îøèáîê è óäåðæàòü ïîëåò èõ òâîð÷åñêîé ôàíòàçèè â íàäëåæàùèõ ãðàíèöàõ. Îäíàêî, ïîä÷åðêèâàë Êàíòîð, ìåòîäîëîãè÷åñêèå ïðèíöèïû êîíöåïöèè Êðîíåêåðà íå ÿâëÿþòñÿ ïëîäîòâîðíûìè. “Ìû íå îáÿçàíû èì íèêàêèìè èñòèííûìè óñïåõàìè è, åñëè áû ìû â äåéñòâèòåëüíîñòè òî÷íî ðóêîâîäñòâîâàëèñü èìè, òî ðàçâèòèå íàóêè îñòàíîâèëîñü áû èëè áûëî ââåäåíî â ñàìûå óçêèå ãðàíèöû.” Âïðî÷åì, çàìåòèë Êàíòîð, îêîí÷àòåëüíîå ñóæäåíèå î êîíöåïöèè Êðîíåêåðà ñòàíåò âîçìîæíûì ëèøü òîãäà, êîãäà îíà áóäåò ðàçðàáîòàíà â öåëîì è â äåòàëÿõ, â ñâÿçè ñ ÷åì âûÿñíèòñÿ å¸ îòíîøåíèå ê ãåîìåòðèè è ìåõàíèêå. Ïîêà ýòîãî åù¸ íåò, ïðèãîäíîñòü êîíöåïöèè Êðîíåêåðà íå ìîæåò áûòü íàçâàíà äîñòàòî÷íî îáîñíîâàííîé.
Êðèòè÷åñêèå çàìå÷àíèÿ Êàíòîðà â àäðåñ êîíöåïöèè Êðîíåêåðà èìåþò ìåòîäîëîãè÷åñêèì ñòåðæíåì åãî òðåòüå “îãðàíè÷èòåëüíîå òðåáîâàíèå”. Îíè âåðíû è íå ïîòåðÿëè ñâîåãî çíà÷åíèÿ äî íàøåãî âðåìåíè. Íî âðÿä ëè ìîæíî íàçâàòü ïðàâèëüíûì ñëåäóþùèå êðèòè÷åñêèå çàìå÷àíèÿ Êàíòîðà, êîòîðûå îí, ïî-âèäèìîìó, ñ÷èòàë íàèáîëåå ñåðüåçíûìè: ìîùíîñòü êîíòèíóóìà âûøå ìîùíîñòè ìíîæåñòâà íàòóðàëüíûõ ÷èñåë. Ñëåäîâàòåëüíî, çàïàñ íàòóðàëüíûõ ÷èñåë íåäîñòàòî÷åí äëÿ îïèñàíèÿ òî÷åê âðåìåííîãî è ïðîñòðàíñòâåííîãî êîíòèíóóìà, ïîýòîìó êîíöåïöèÿ Êðîíåêåðà íå ìîæåò ñ÷èòàòüñÿ ñîâåðøåííîé. Ýòà àðãóìåíòàöèÿ êàíòîðà îáëàäàåò äîêàçàòåëüíîé ñèëîé ëèøü äëÿ ïðèâåðæåíöåâ ó÷åíèÿ î ñ÷åòíûõ è íåñ÷åòíûõ ìíîæåñòâàõ; åãî ïðîòèâíèêè ñ÷èòàòüñÿ ñ ýòîé àðãóìåíòàöèåé Êàíòîðà íå îáÿçàíû.
Èäåè Êðîíåêåðà â íåêîòîðîé ìåðå ñïîñîáñòâîâàëè ñíà÷àëà îôîðìëåíèþ êîíöåïöèè èíòóèöèîíèçìà, à ïîòîì è êîíñòðóêòèâíîé ìàòåìàòèêè.
Äî ïîñëåäíåãî äåñÿòèëåòèÿ XIX âåêà ìàòåìàòèêè, ëîãèêè è ôèëîñîôû ïðèçíàâàëè ïîíÿòèÿ èððàöèîíàëüíîãî ÷èñëà, íî îòðèöàëè ïîíÿòèå àêòóàëüíîé áåñêîíå÷íîñòè; îíè ñ÷èòàëè åãî âíóòðåííå ïðîòèâîðå÷èâûì. Íåêîòîðûå èç íèõ ïûòàëèñü ýòî äîêàçàòü. Êàíòîð èçó÷èë ìåòîäîëîãè÷åñêóþ îñíîâó òàêèõ äîêàçàòåëüñòâ è ïîêàçàë èõ ïîëíóþ íåñîñòîÿòåëüíîñòü.
“Âñå òàê íàçûâàåìûå äîêàçàòåëüñòâà ïðîòèâ âîçìîæíîñòè àêòóàëüíî áåñêîíå÷íûõ ÷èñåë,— ïèñàë Êàíòîð,— îøèáî÷íû, ïîòîìó, ÷òî îíè çàðàíåå ïðèïèñûâàþò èëè, ñêîðåå, íàâÿçûâàþò ðàññìàòðèâàåìûì ÷èñëàì âñå ñâîéñòâà êîíå÷íûõ ÷èñåë
. Ìåæäó òåì, áåñêîíå÷íûå ÷èñëà — åñëè òîëüêî èõ äîëæíî ìûñëèòü â êàêîé-íèáóäü ôîðìå — äîëæíû îáðàçîâàòü áëàãîäàðÿ ñâîåé ïðîòèâîïîëîæíîñòè ê êîíå÷íûì ÷èñëàì ñîâåðøåííî íîâûé ÷èñëîâîé âèä, ñâîéñòâà êîòîðîãî âïîëíå çàâèñÿò îò ïðèðîäû âåùåé è îáðàçóþò ïðåäìåò èññëåäîâàíèÿ, à íå íàøåãî ïðîèçâîëà èëè íàøèõ ïðåäðàññóäêîâ.”
Çàêëþ÷èòåëüíàÿ ÷àñòü ïðèâåäåííîãî âûñêàçûâàíèÿ Êàíòîðà ÿâëÿåòñÿ òî÷íîé õàðàêòåðèñòèêîé ñóùåñòâà ìåòîäîëîãèè åãî íàó÷íûõ èññëåäîâàíèé. Îíà ïîêàçûâàåò, ÷òî èçáðàííûé Êàíòîðîì ïóòü îáîñíîâàíèÿ íàó÷íîé ñàìîñòîÿòåëüíîñòè ó÷åíèÿ î ìíîæåñòâàõ ÿâëÿåòñÿ, ïî ñóòè, ìàòåðèàëèñòè÷åñêèì; îí ìîæåò áûòü ñîãëàñîâàí ñ èäåàëèçìîì (ñóáúåêòèâíûì èëè îáúåêòèâíûì — áåçðàçëè÷íî) òîëüêî íà ñëîâàõ, à íà äåëå ïðîòèâîðå÷èò åìó. Ñòðåìëåíèå Êàíòîðà îáîñíîâàòü ñ ôèëîñîôñêèõ ïîçèöèé âîçìîæíîñòü òàêîé ñîãëàñîâàííîñòè è îáóñëîâèëî äâîéñòâåííîñòü åãî ôèëîñîôñêèõ ïîçèöèé â ïîíèìàíèè ïðèðîäû ìàòåìàòèêè è å¸ ìåòîäîâ.
Íàðÿäó ñ óêàçàííûìè âûøå òðóäíîñòÿìè ïîñòðîåíèÿ òåîðèè ìíîæåñòâ â íåé áûëè îáíàðóæåíû ïàðàäîêñû
(àíòèíîìèè) ïîñòàâèâøèå ïîä ñîìíåíèå ó÷åíèå Ã. Êàíòîðà â öåëîì
. Ýòè ïàðàäîêñû ñòàëè îáúåêòîì îñîáîãî âíèìàíèÿ ìàòåìàòèêîâ. È, êîíå÷íî, íå ñëó÷àéíî. Êàê óêàçûâàëîñü âûøå, åù¸ ïðè æèçíè Êàíòîðà åãî òåîðèÿ ìíîæåñòâ ñòàëà ôóíäàìåíòîì âñåãî çäàíèÿ ìàòåìàòèêè, à å¸ ìåòîäû — äåéñòâåííûì îðóäèåì ðàçâèòèÿ ìíîãèõ âåäóùèõ ìàòåìàòè÷åñêèõ òåîðèé.
Ïåðâûé ïàðàäîêñ îáíàðóæèë ñàì Êàíòîð â 1895 ãîäó è ñîîáùèë î íåì â ïèñüìå ê Ãèëüáåðòó. ÷åðåç äâà ãîäà ýòîò ïàðàäîêñ îáíàðóæèë Áóðàëè-Ôîðòè; îí ñäåëàë åãî äîñòîÿíèåì âñåõ ìàòåìàòèêîâ.
Парадокс Бурали-Форти.
Ïóñòü Ð
— ìíîæåñòâî âñåõ ïîðÿäêîâûõ ÷èñåë. Ýòî ìíîæåñòâî âïîëíå óïîðÿäî÷åíî; ñëåäîâàòåëüíî, îíî îïðåäåëÿåò íåêîòîðîå îðäèíàðíîå òðàíñôèíèòíîå ÷èñëî ð
. Åñëè Ðð
— ìíîæåñòâî ïîðÿäêîâûõ ÷èñåë ìåíüøå ð
, òî Ðð
èìååò òîò æå ïîðÿäêîâûé òèï, ÷òî è Ð
. Íî Ðð
— îòðåçîê ìíîæåñòâà Ð
, îïðåäåëÿåìûé ÷èñëîì ð
. Ñëåäîâàòåëüíî Ð
è åãî îòðåçîê Ðð
ïîäîáíû äðóã äðóãó. Íî Êàíòîð äîêàçàë, ÷òî âïîëíå óïîðÿäî÷åííîå ìíîæåñòâî íå ìîæåò áûòü ïîäîáíî ëþáîìó ñâîåìó îòðåçêó.
 1899 ãîäó Êàíòîð îòêðûë åù¸ îäèí ïàðàäîêñ è ñîîáùèë î íåì Ð. Äåäåêèíäó.  1901 ãîäó ýòîò ïàðàäîêñ ïðèâëåê âíèìàíèå Á. Ðàññåëà.
Парадокс Кантора.
Ïóñòü N
— ìíîæåñòâî âñåõ âîçìîæíûõ ìíîæåñòâ, S
—ìíîæåñòâî âñåõ âîçìîæíûõ ïîäìíîæåñòâ ìíîæåñòâà N
. Ïîñêîëüêó ìîùíîñòü ìíîæåñòâà âñåõ âîçìîæíûõ ïîäìíîæåñòâ ëþáîãî ìíîæåñòâà èìååò ìîùíîñòü, áîëüøóþ ìîùíîñòè ýòîãî ìíîæåñòâà, òî ìîùíîñòü S
äîëæíà áûòü áîëüøå ìîùíîñòè N
. Ñ äðóãîé ñòîðîíû, ìíîæåñòâî N
åñòü ìíîæåñòâî âñåõ âîçìîæíûõ ìíîæåñòâ; ñëåäîâàòåëüíî S
ÿâëÿåòñÿ ïîäìíîæåñòâîì N
. Íî ìîùíîñòü ïîäìíîæåñòâà íå áîëüøå ìîùíîñòè ìíîæåñòâà; çíà÷èò ìîùíîñòü S
íå áîëüøå ìîùíîñòè N
.
Íàèáîëüøóþ èçâåñòíîñòü ïðèîáðåë ïàðàäîêñ, îòêðûòûé Á. Ðàññåëîì â 1902 ãîäó è îïóáëèêîâàííûé èì â 1903 ãîäó. Ýòîò ïàðàäîêñ îòêðûë è Ý. Öåðìåëî, íî â ïå÷àòè åãî íå îïóáëèêîâàë.
Парадокс Рассела.
Î íåêîòîðûõ ìíîæåñòâàõ ìîæíî ñêàçàòü, ÷òî îíè ñîäåðæàò ñåáÿ â êà÷åñòâå ñâîåãî ýëåìåíòà; òàêîâî, íàïðèìåð, ìíîæåñòâî âñåõ ìíîæåñòâ. Ðàñïðåäåëèì âñå âîçìîæíûå ìíîæåñòâà íà äâà êëàññà. Ê ïåðâûì îòíåñåì òå ìíîæåñòâà, êîòîðûå íå ñîäåðæàò ñåáÿ â êà÷åñòâå ñâîèõ ýëåìåíòîâ. Êî âòîðîìó îòíåñåì âñå îñòàëüíûå, ò. å. êîòîðûå ñîäåðæàò ñåáÿ â êà÷åñòâå ñâîèõ ýëåìåíòîâ. Ðàññìîòðèì ïåðâûé êëàññ ìíîæåñòâ. Ýòîò êëàññ ìíîæåñòâ â ñâîþ î÷åðåäü ÿâëÿåòñÿ íåêîòîðûì ìíîæåñòâîì N
, à ïîòîìó ïðèíàäëåæèò ê ïåðâîìó èëè êî âòîðîìó êëàññó.
Äîïóñòèì, ÷òî ìíîæåñòâî N
ïðèíàäëåæèò ê ïåðâîìó êëàññó. Ïåðâûé êëàññ — ýòî êëàññ ìíîæåñòâ, êàæäîå èç êîòîðûõ íå ñîäåðæèò ñåáÿ â êà÷åñòâå ýëåìåíòà. Íî åñëè N
ïðèíàäëåæèò ê ïåðâîìó êëàññó, òî òàê êàê ìíîæåñòâî N
åñòü ìíîæåñòâî âñåõ ìíîæåñòâ ïåðâîãî êëàññà, îíî äîëæíî ñîäåðæàòü è ñåáÿ â êà÷åñòâå ýëåìåíòà. Èòàê, åñëè ìíîæåñòâî N
íå ñîäåðæèò ñåáÿ â êà÷åñòâå ýëåìåíòà, òî îíî ñîäåðæèò ñåáÿ â êà÷åñòâå ýëåìåíòà, ñëåäîâàòåëüíî íåëüçÿ ïðåäïîëàãàòü, ÷òî ìíîæåñòâî N
ïðèíàäëåæèò ê ïåðâîìó êëàññó.
Ïðåäïîëîæèì òåïåðü, ÷òî ìíîæåñòâî N
ïðèíàäëåæèò êî âòîðîìó êëàññó, ò. å. ñîäåðæèò ñåáÿ â êà÷åñòâå ýëåìåíòà. Íî ýëåìåíòàìè ìíîæåñòâà N
ÿâëÿþòñÿ òîëüêî ìíîæåñòâà, íå ñîäåðæàùèå ñåáÿ â êà÷åñòâå ýëåìåíòà. Ñëåäîâàòåëüíî, åñëè N
ñîäåðæèò ñåáÿ â êà÷åñòâå ýëåìåíòà, òî N
íå ñîäåðæèò ñåáÿ â êà÷åñòâå ýëåìåíòà. Ìû îïÿòü ïðèøëè ê ïðîòèâîðå÷èþ è âûíóæäåíû ïðèçíàòü, ÷òî ìíîæåñòâî N
íå ìîæåò íè ïðèíàäëåæàòü, íè íå ïðèíàäëåæàòü ê ïåðâîìó êëàññó.
 íàøå âðåìÿ èçâåñòíû è äðóãèå ïàðàäîêñû.
Ñ íà÷àëà XX âåêà è äî íàøèõ äíåé íå ïðåêðàùàþòñÿ ïîïûòêè ïðåîäîëåòü òðóäíîñòè, ñâÿçàííûå ñ ïîñòðîåíèåì è ïàðàäîêñàìè òåîðèè ìíîæåñòâ. Óñòàíîâëåííûå â ýòîì íàïðàâëåíèè ðåçóëüòàòû íå ïîëó÷èëè, îäíàêî, âñåîáùåãî ïðèçíàíèÿ. Åñëè è ìîæíî ãîâîðèòü î öåííûõ ðåçóëüòàòàõ, çäåñü íàéäåííûõ, òî â ïåðâóþ î÷åðåäü â ñâÿçè ñ ðàçëè÷íûìè âàðèàíòàìè àêñèîìàòè÷åñêîãî ïîñòðîåíèÿ òåîðèè ìíîæåñòâ.
Âïåðâûå àêñèîìàòè÷åñêîå ïîñòðîåíèå òåîðèè ìíîæåñòâ îñóùåñòâèë Ý. Öåðìåëî â 1908 ãîäó. Âïîñëåäñòâèè àêñèîíîìàòèêà Öåðìåëî áûëà äîïîëíåíà è âèäîèçìåíåíà â ðàáîòàõ À. Ôðåíêåëÿ (1922, 1925), Ò. Ñêîëåìà (1922-1923, 1929), Äæ. Íåéìàíà (1925, 1928), Ï. Áåðíàéñà (1937-1954) è äðóãèõ ìàòåìàòèêîâ. Òàê, Ôðåíêåëü äîïîëíèë àêñèîíîìàòèêó Öåðìåëî îäíîé àêñèîìîé, ïîñëå ÷åãî ïîëó÷èëàñü íîâàÿ ñèñòåìà àêñèîì — å¸ íàçâàëè ñèñòåìîé Öåðìåëî-Ôðåíêåëÿ — áîëåå ñèëüíàÿ, ÷åì èñõîäíàÿ ñèñòåìà àêñèîì Öåðìåëî.  îòëè÷èå îò ñèñòåìû Öåðìåëî, îáîçíà÷àåìîé îáû÷íî áóêâîé Z, ñèñòåìó Öåðìåëî-Ôðåíêåëÿ îáîçíà÷àþò äâóìÿ áóêâàìè: ZF. Ñ ïîìîùüþ ZF ìîæíî ïîëó÷èòü ðÿä ôóíäàìåíòàëüíûõ ðåçóëüòàòîâ, íå äîêàçóåìûõ ñ ïîìîùüþ Z.
Öåðìåëî ñôîðìóëèðîâàë ñèñòåìó àêñèîì, â êîòîðîé îïèñàë íåêîòîðûå ñâîéñòâà ìíîæåñòâ. Îñòàëüíûå ñâîéñòâà ìíîæåñòâ, óñòàíîâëåííûå â òåîðèè ìíîæåñòâ Êàíòîðà, Öåðìåëî ïûòàëñÿ âûâåñòè èç ñâîèõ àêñèîì.
Îñíîâíîé çàìûñåë Öåðìåëî ñîñòîÿë â òîì, ÷òîáû îãðàíè÷èòü îáëàñòü ïðèìåíåíèÿ àêñèîíîìàòèêè Z òîëüêî òàêèìè ìíîæåñòâàìè, ðàññìîòðåíèå êîòîðûõ íå ïðèâîäèò ê ïàðàäîêñàì. Âïîñëåäñòâèè, ïðè ðàçðàáîòêå íîâûõ âàðèàíòîâ àêñèîíîìàòèêè òåîðèè ìíîæåñòâ, ýòà îãðàíè÷èòåëüíàÿ òåíäåíöèÿ ïîëó÷èëà âñåîáùåå ïðèçíàíèå. Ïîçâîëèòåëüíî, îäíàêî, äóìàòü, ÷òî â îäíîì ñóùåñòâåííîì ïóíêòå îíà íå îòâå÷àåò îñíîâíûì óñòàíîâêàì è çàìûñëó ñàìîãî Ã. Êàíòîðà. Êàíòîð ñòðåìèëñÿ ðàçâèòü òåîðèþ ìíîæåñòâ âî âñåé îáùíîñòè, êàê òåîðèþ, îòíîñÿùóþñÿ ê ëþáûì ìíîæåñòâàì; íàçâàííàÿ îãðàíè÷èòåëüíàÿ òåíäåíöèÿ áûëà äëÿ íåãî ñîâåðøåííî ÷óæäîé.
Åñëè ïðèíÿòü ñèñòåìó Z, òî â íåêîòîðûõ ñóùåñòâåííûõ ïóíêòàõ òåîðèÿ ìíîæåñòâ Êàíòîðà ïîëó÷èò äîñòàòî÷íîå îáîñíîâàíèå. Îáóñëîâëèâàåòñÿ ýòî ñëåäóþùèìè ïðè÷èíàìè.  ñèñòåìå Öåðìåëî èìååòñÿ òàê íàçûâàåìàÿ àêñèîìà âûáîðà (ðàíüøå å¸ îáû÷íî íàçûâàëè ïðîñòî àêñèîìîé Öåðìåëî: â äàëüíåéøåì ìû ÷àñòî áóäåì íàçûâàòü å¸ èìåííî òàê):
Åñëè äàíî ìíîæåñòâî Ì, ñîñòîÿùåå èç ìíîæåñòâ N, íå ïóñòûõ è áåç îáùèõ ýëåìåíòîâ, òî èç êàæäîãî ìíîæåñòâà N ìîæíî âûáðàòü ïî îäíîìó ýëåìåíòó; ñîâîêóïíîñòü âûáðàííûõ ýëåìåíòîâ îáðàçóåò íîâîå ìíîæåñòâî Ð.
Âïîñëåäñòâèè îðòîäîêñàëüíûå ïîñëåäîâàòåëè Ã. Êàíòîðà íåðåäêî èçìåíÿëè ôîðìóëèðîâêó àêñèîìû Öåðìåëî òàê, ÷òî îíà ñòàíîâèëàñü óòâåðæäåíèåì ñóùåñòâîâàíèÿ: Äëÿ êàæäîãî ìíîæåñòâà Ì ìíîæåñòâ N, íå ïóñòûõ è íå èìåþùèõ îáùèõ ýëåìåíòîâ, ñóùåñòâóåò (ïî êðàéíåé ìåðå îäíî) ìíîæåñòâî Ð, ñîäåðæàùåå ïî îäíîìó è òîëüêî îäíîìó ýëåìåíòó èç êàæäîãî ìíîæåñòâà N.
Óòâåðæäåíèå ñóùåñòâîâàíèÿ ìíîæåñòâà Ð
ïîíèìàëîñü, êîíå÷íî, â ñìûñëå Êàíòîðà.
Îïèðàÿñü íà ýòó àêñèîìó Öåðìåëî äîêàçàë, ÷òî âñÿêîå ìíîæåñòâî ìîæåò áûòü ïðåäñòàâëåíî â ôîðìå âïîëíå óïîðÿäî÷åííîãî ìíîæåñòâà, ò. å., ÷òî ìîùíîñòü ëþáîãî ìíîæåñòâà åñòü àëåîð
. Êàê óêàçûâàëîñü âûøå, ýòîò ôàêò îáåñïå÷èâàåò âîçìîæíîñòü ïîñòðîåíèÿ àðèôìåòèêè êàðäèíàëüíûõ òðàíñôèíèòíûõ ÷èñåë ïî÷òè âî âñåé îáùíîñòè. Äîñòàòî÷íî ñêàçàòü, ÷òî àêñèîìà Öåðìåëî ïîçâîëÿåò ðåøèòü â óòâåðäèòåëüíîì ñìûñëå ïðîáëåìó òðèõîòîìèè è äàåò îáîñíîâàíèå òðàíñôèíèòíîé èíäóêöèè. Òîëüêî ãèïîòåçà êîíòèíóóìà îñòàâàëàñü ïî ïðåæíåìó çàãàäêîé. Öåðìåëî ìîã óòâåðæäàòü, ÷òî ìîùíîñòü êîíòèíóóìà åñòü àëåîð, íî êàêîå ìåñòî íà øêàëå àëåîðîâ çàíèìàåò Ñ
— ýòî îñòàâàëîñü íåèçâåñòíûì. Ê ýòîìó ìîæíî òîëüêî ïðèáàâèòü, ÷òî äîêàçàòåëüñòâà ýêâèâàëåíòíîñòè äðóã äðóãó íåêîòîðûõ ôîðì ãèïîòåçû êîíòèíóóìà òàêæå îïèðàþòñÿ íà àêñèîìó Öåðìåëî.
Áîëåå äåñÿòè ëåò ñ ìîìåíòà îïóáëèêîâàíèÿ ìåìóàðîâ Öåðìåëî ïðèëîæåíèÿ àêñèîìû âûáîðà îãðàíè÷èâàëèñü îáëàñòüþ òåîðèè ôóíêöèé äåéñòâèòåëüíîãî ïåðåìåííîãî. Êðîìå óêàçàííûõ, ìîæíî, íàïðèìåð, óïîìÿíóòü ïðèëîæåíèÿ ýòîé àêñèîìû â òåîðèè òî÷å÷íûõ ìíîæåñòâ è, â ÷àñòíîñòè, â òåîðèè èçìåðèìûõ ìíîæåñòâ.
 20-õ è 30-õ ãîäàõ ÕÕ âåêà ïîëå ïðèëîæåíèÿ àêñèîìû Öåðìåëî çíà÷èòåëüíî ðàñøèðèëîñü. Ìîæíî, íàïðèìåð, óêàçàòü íà èññëåäîâàíèÿ Áèðêãîôà ñèñòåì äèôôåðåíöèàëüíûõ óðàâíåíèé, â êîòîðûõ îí ïðèìåíÿë òðàíñôèíèòíóþ èíäóêöèþ. Îñîáåííî âàæíî óêàçàòü íà òåîðèþ ëèíåéíûõ îïåðàòîðîâ, êîòîðóþ Æ. Àäàìàð â íà÷àëå 30-õ ãîäîâ íàçûâàë íàèáîëåå ñèëüíûì ìåòîäîì èññëåäîâàíèÿ ñîâðåìåííîé ìàòåìàòèêè. Òåîðèÿ ëèíåéíûõ îïåðàòîðîâ ðàçâèâàåòñÿ íà áàçå îáùåãî ó÷åíèÿ î ìíîæåñòâàõ è ïîëüçóåòñÿ àêñèîìîé Öåðìåëî äëÿ óñòàíîâëåíèÿ íåêîòîðûõ âàæíåéøèõ ñâîèõ ïðåäëîæåíèé. Øèðîêîå ïîëå äëÿ ïðèìåíåíèÿ àêñèîìû Öåðìåëî äàëè àëãåáðà è òîïîëîãèÿ.
Ñâîåîáðàçèå àêñèîìû Öåðìåëî çàêëþ÷àåòñÿ â òîì, ÷òî îíà íå òîëüêî ÿâëÿåòñÿ îðóäèåì îòûñêàíèÿ íîâûõ ìàòåìàòè÷åñêèõ ôàêòîâ è ïðèäàåò èçâåñòíóþ îáùíîñòü ó÷åíèþ î ìíîæåñòâàõ, íî è óñóãóáëÿåò òðóäíîñòè
îáîñíîâàíèÿ ìàòåìàòèêè.
Îäíà èç òðóäíîñòåé ñîñòîèò â òîì, ÷òî, ðàññìàòðèâàÿ âïîëíå îïðåäåëåííûå (â ñìûñëå Êàíòîðà) ìíîæåñòâà, ñ ïîìîùüþ àêñèîìû Öåðìåëî ìîæíî äîêàçàòü ñóùåñòâîâàíèå ìíîæåñòâ, íåîïðåäåëèìûõ â ñìûñëå Êàíòîðà. Âîò ïðèìåð.
Ðàññìîòðèì âñå ôóíêöèè äåéñòâèòåëüíîãî ïåðåìåííîãî õ
, îïðåäåëåííûå íà ñåãìåíòå [0, 1] è íå ðàâíûå íà ýòîì ñåãìåíòå òîæäåñòâåííî íóëþ. Ðàçäåëèì ýòè ôóíêöèè íà ïàðû, îòíîñÿ â îäíó ïàðó òàêèå äâå ôóíêöèè, êîòîðûå îòëè÷àþòñÿ òîëüêî çíàêîì, ò. å. ôóíêöèè f(x)ï–f(x)
. Ïî àêñèîìå Öåðìåëî ñóùåñòâóåò ìíîæåñòâî Ð
, âêëþ÷àþùåå ïî îäíîé è òîëüêî îäíîé ôóíêöèè êàæäîé ïàðû. Ñëåäîâàòåëüíî, ñîãëàñíî àêñèîìå Öåðìåëî, ìîæíî óòâåðæäàòü ñóùåñòâîâàíèå Ð
ôóíêöèé äåéñòâèòåëüíîãî ïåðåìåííîãî õ
, îïðåäåëÿåìûõ íà ñåãìåíòå [0, 1] è íå ðàâíûõ íà ýòîì ñåãìåíòå òîæäåñòâåííî íóëþ, òàêîãî, ÷òî
à) êàêîâû áû íè áûëè ôóíêöèè f1
è f2
ìíîæåñòâà Ð
, âñåãäà  ; ;
á) êàêîâà áû íè áûëà ôóíêöèÿ j(õ)
, îïðåäåëåííàÿ íà ñåãìåíòå [0, 1] è íå ðàâíàÿ íà íåì òîæäåñòâåííî íóëþ, ñóùåñòâóåò îäíà è òîëüêî îäíà ôóíêöèÿ f
ìíîæåñòâà Ð
, òàêàÿ, ÷òî ëèáî f+
j=
0, ëèáî f–
j=
0 äëÿ ëþáîãî õ
,  . .
Îäíàêî ìíîæåñòâî Ð
íå îïðåäåëåíî â ñìûñëå Êàíòîðà, òàê êàê ìû íå ìîæåì ñêàçàòü î ëþáîé ôóíêöèè j(õ)
, ïîä÷èíÿþùåéñÿ âûñòàâëåííûì óñëîâèÿì, ïðèíàäëåæèò ëè îíà Ð
èëè íå ïðèíàäëåæèò.
Äðóãàÿ òðóäíîñòü ñîñòîèò â òîì, ÷òî ñ ïîìîùüþ àêñèîìû Öåðìåëî ÷àñòî âîçìîæíî îïðåäåëèòü êëàññ ìíîæåñòâ, â òî âðåìÿ êàê íè îäíîãî îáúåêòà èç ýòîãî êëàññà îïðåäåëèòü (ðàçëè÷èòü) íå óäàåòñÿ. Íàïðèìåð, ñîãëàñíî àêñèîìå Öåðìåëî ñóùåñòâóåò êëàññ íåèçìåðèìûõ ìíîæåñòâ. Îäíàêî äî ñèõ ïîð íèêòî íå ñìîã ïîñòðîèòü (äàòü) èíäèâèäóàëüíîãî ïðèìåðà íåèçìåðèìîãî ìíîæåñòâà.
 êîíöå XIX è íà÷àëå ÕÕ âåêà èññëåäîâàíèÿ ïî âîïðîñàì îáîñíîâàíèÿ ìàòåìàòèêè èìåëè ïðåèìóùåñòâåííî ïðåîäîëåíèå ñëåäóþùèõ îñíîâíûõ òðóäíîñòåé.
Òåîðèÿ ìíîæåñòâ ñòàëà â ýòî âðåìÿ ôóíäàìåíòîì ìàòåìàòèêè, à å¸ ìåòîäû — îñíîâîé ìåòîäîâ âåäóùèõ ìàòåìàòè÷åñêèõ äèñöèïëèí. Âìåñòå ñ òåì ñàìà òåîðèÿ ìíîæåñòâ îêàçàëàñü íåîáîñíîâàííîé â ðÿäå ðåøàþùèõ ïóíêòîâ (ãèïîòåçà êîíòèíóóìà, ïðîáëåìà óïîðÿäî÷èâàíèÿ).
 òåîðèè ìíîæåñòâ áûëè îáíàðóæåíû ïàðàäîêñû (àíòèíîìèè), óñòðàíåíèå êîòîðûõ — êàê ïîêàçàëè èññëåäîâàíèÿ ìàòåìàòèêîâ è ëîãèêîâ, íà÷èíàÿ ñ Ðàññåëà — îêàçàëîñü îòíþäü íå ïðîñòûì äåëîì.
Ïàðàäîêñû òåîðèè ìíîæåñòâ îêàçàëèñü èìåþùèìè íå òîëüêî ìàòåìàòè÷åñêóþ, íî è ëîãè÷åñêóþ ïðèðîäó; â ýòîé ñâÿçè åñòåñòâåííî âîçíèê âîïðîñ î ñðåäñòâàõ ëîãèêè, äîïóñòèìûõ â ìàòåìàòèêå.
Ýòè òðóäíîñòè ïîñòàâèëè ïåðåä ìàòåìàòèêàìè ïðîáëåìó ïîíèìàíèÿ ñóùåñòâîâàíèÿ â ïðèìåíåíèè ê ìàòåìàòè÷åñêèì îáúåêòàì.
×òîáû ëó÷øå óÿñíèòü ñìûñë ïðîáëåìû ñóùåñòâîâàíèÿ, óñòàíîâè ñíà÷àëà ðàçëè÷èå ìåæäó òàê íàçûâàåìûìè ýôôåêòèâíûìè è íåýôôåêòèâíûìè äîêàçàòåëüñòâàìè ñóùåñòâîâàíèÿ. Ýòè ðàçëè÷èÿ ìû ïîñòàðàåìñÿ îïèñàòü ñîîòâåòñòâåííî ïðåäñòàâëåíèÿì, ãîñïîäñòâîâàâøèõ â ìàòåìàòèêå ïðèìåðíî äî êîíöà 20-õ — íà÷àëà 40-õ ãîäîâ ÕÕ âåêà.
Äîêàæåì, ÷òî êàêîâû áû íè áûëè íàòóðàëüíûå ÷èñëà Ð1
, …, Ðï
, ñóùåñòâóåò íàòóðàëüíîå ÷èñëî Ð
, âçàèìíî ïðîñòîå ñ êàæäûì èç ýòèõ ÷èñåë. Ðàññìîòðèì ÷èñëî Ð=Ð1
*…*Ðï
+1; ïðè äåëåíèè íà ëþáîå èç ÷èñåë Ð1
, …, Ðï
ýòî ÷èñëî äàåò â îñòàòêå 1. Ñëåäîâàòåëüíî, îíî âçàèìíî ïðîñòîå ñ êàæäûì èç ÷èñåë Ð1
, …, Ðï
. Èòàê, ÷èñëî Ð
ñóùåñòâóåò.
Ýòî äîêàçàòåëüñòâî ýôôåêòèâíî. Ìû äîêàçàëè ñóùåñòâîâàíèå ÷èñëà Ð
òåì, ÷òî ïîêàçàëè, êàê ñ ïîìîùüþ îáû÷íûõ àðèôìåòè÷åñêèõ äåéñòâèé íàéòè ýòî ÷èñëî. Ê ÷èñëó ýôôåêòèâíûõ äîêàçàòåëüñòâ îòíîñÿòñÿ òàêæå äîêàçàòåëüñòâà ôîðìóë äëÿ ðåøåíèÿ àëãåáðàè÷åñêèõ óðàâíåíèé òðåòüåé è ÷åòâåðòîé ñòåïåíåé, äîêàçàòåëüñòâî ñóùåñòâîâàíèÿ îïðåäåëåííîãî èíòåãðàëà îò íåïðåðûâíîé ôóíêöèè è ò. ï. Ïðè ýòîì, åñòåñòâåííî, ñ÷èòàþòñÿ îáîñíîâàííûìè ñîîòâåòñòâóþùèå àëãåáðàè÷åñêèå îïåðàöèè, àðèôìåòèêà äåéñòâèòåëüíûõ ÷èñåë è îïåðàöèÿ ïåðåõîäà ê ïðåäåëó.
Âîîáùå âñÿêîå ýôôåêòèâíîå äîêàçàòåëüñòâî òåì è õàðàêòåðèçóåòñÿ, ÷òî ñ ïîìîùüþ òàê èëè èíà÷å îáîñíîâàííûõ ïîñûëîê îíî ïîçâîëÿåò èíäèâèäóàëüíî îõàðàêòåðèçîâàòü
(âû÷èñëèòü, ïîñòðîèòü è ò. ï.) îáúåêò, ñóùåñòâîâàíèå êîòîðîãî äîêàçûâàþò.
Ðàññìîòðèì òåïåðü äðóãîé ïðèìåð. ÷èñëî íàçûâàåòñÿ àëãåáðàè÷åñêèì, åñëè îíî ÿâëÿåòñÿ êîðíåì êàêîãî-ëèáî àëãåáðàè÷åñêîãî óðàâíåíèÿ ñ öåëûìè êîýôôèöèåíòàìè. Íàïðèìåð, ÷èñëî  àëãåáðàè÷åñêîå, ò. ê. îíî ÿâëÿåòñÿ êîðíåì óðàâíåíèÿ õ
2
–2=0. Íàïðîòèâ, ÷èñëî, íå óäîâëåòâîðÿþùåå íèêàêîìó àëãåáðàè÷åñêîìó óðàâíåíèþ ñ öåëûìè êîýôôèöèåíòàìè, íàçûâàåòñÿ òðàíñöåíäåíòíûì ÷èñëîì. Äîêàæåì, ñëåäóÿ Êàíòîðó, ñóùåñòâîâàíèå òðàíñöåíäåíòíûõ ÷èñåë. Èçâåñòíî, ÷òî ìíîæåñòâî âñåõ àëãåáðàè÷åñêèõ ÷èñåë ñ÷¸òíî, â òî âðåìÿ êàê ìíîæåñòâî âñåõ äåéñòâèòåëüíûõ ÷èñåë íåñ÷¸òíî. Åñëè áû òðàíñöåíäåíòíûå ÷èñëà íå ñóùåñòâîâàëè, êàæäîå äåéñòâèòåëüíîå ÷èñëî áûëî áû àëãåáðàè÷åñêèì è, ñëåäîâàòåëüíî, ìíîæåñòâî âñåõ äåéñòâèòåëüíûõ ÷èñåë áûëî áû ñ÷åòíûì. ÷òîáû èçáåæàòü ïðîòèâîðå÷èÿ îñòàåòñÿ ïðèíÿòü, ÷òî òðàíñöåíäåíòíûå ÷èñëà ñóùåñòâóþò, õîòü äîêàçàòåëüñòâî íå äàåò íàì íè îäíîãî ïðèìåðà òðàíñöåíäåíòíîãî ÷èñëà. Ýòî ïðèìåð íåýôôåêòèâíîãî äîêàçàòåëüñòâà.  íåýôôåêòèâíûõ äîêàçàòåëüñòâàõ ñóùåñòâîâàíèÿ (îñíîâàííûå, íàïðèìåð, íà ïðèíöèïå èñêëþ÷åííîãî òðåòüåãî) íå äàåòñÿ íèêàêîãî ïðèìåðà îáúåêòîâ, ñóùåñòâîâàíèå êîòîðûõ äîêàçûâàåòñÿ. àëãåáðàè÷åñêîå, ò. ê. îíî ÿâëÿåòñÿ êîðíåì óðàâíåíèÿ õ
2
–2=0. Íàïðîòèâ, ÷èñëî, íå óäîâëåòâîðÿþùåå íèêàêîìó àëãåáðàè÷åñêîìó óðàâíåíèþ ñ öåëûìè êîýôôèöèåíòàìè, íàçûâàåòñÿ òðàíñöåíäåíòíûì ÷èñëîì. Äîêàæåì, ñëåäóÿ Êàíòîðó, ñóùåñòâîâàíèå òðàíñöåíäåíòíûõ ÷èñåë. Èçâåñòíî, ÷òî ìíîæåñòâî âñåõ àëãåáðàè÷åñêèõ ÷èñåë ñ÷¸òíî, â òî âðåìÿ êàê ìíîæåñòâî âñåõ äåéñòâèòåëüíûõ ÷èñåë íåñ÷¸òíî. Åñëè áû òðàíñöåíäåíòíûå ÷èñëà íå ñóùåñòâîâàëè, êàæäîå äåéñòâèòåëüíîå ÷èñëî áûëî áû àëãåáðàè÷åñêèì è, ñëåäîâàòåëüíî, ìíîæåñòâî âñåõ äåéñòâèòåëüíûõ ÷èñåë áûëî áû ñ÷åòíûì. ÷òîáû èçáåæàòü ïðîòèâîðå÷èÿ îñòàåòñÿ ïðèíÿòü, ÷òî òðàíñöåíäåíòíûå ÷èñëà ñóùåñòâóþò, õîòü äîêàçàòåëüñòâî íå äàåò íàì íè îäíîãî ïðèìåðà òðàíñöåíäåíòíîãî ÷èñëà. Ýòî ïðèìåð íåýôôåêòèâíîãî äîêàçàòåëüñòâà.  íåýôôåêòèâíûõ äîêàçàòåëüñòâàõ ñóùåñòâîâàíèÿ (îñíîâàííûå, íàïðèìåð, íà ïðèíöèïå èñêëþ÷åííîãî òðåòüåãî) íå äàåòñÿ íèêàêîãî ïðèìåðà îáúåêòîâ, ñóùåñòâîâàíèå êîòîðûõ äîêàçûâàåòñÿ.
Ïàðàäîêñû òåîðèè ìíîæåñòâ ÿâèëèñü äîïîëíèòåëüíûì (íî íå åäèíñòâåííûì) îñíîâàíèåì ïîñòàâèòü ïîä ñîìíåíèå íå òîëüêî ýôôåêòèâíûå äîêàçàòåëüñòâà ñóùåñòâîâàíèÿ, áàçèðóþùèåñÿ íà àêñèîìå Öåðìåëî, íî è ëþáûå íåýôôåêòèâíûå äîêàçàòåëüñòâà ñóùåñòâîâàíèÿ ìàòåìàòè÷åñêèõ îáúåêòîâ. Ìîæíî ëè, ñïðàøèâàëè ìàòåìàòèêè, âûñêàçûâàâøèå ýòè ñîìíåíèÿ, ñ÷èòàòü ñóùåñòâóþùèì ìàòåìàòè÷åñêèé îáúåêò, êîòîðûé ìû íå óìååì ïîñòðîèòü, ìíîæåñòâî, íå îäíîãî ýëåìåíòà êîòîðîãî ìû íå ñóìååì óêàçàòü?
Êàêîå çíà÷åíèå èìåëè ñîìíåíèÿ â ïðàâîìåðíîñòè íåýôôåêòèâíûõ äîêàçàòåëüñòâ ñóùåñòâîâàíèÿ äëÿ ìàòåìàòèêè íà÷àëà ÕÕ âåêà? Î÷åíü áîëüøîå! Îíè, ïî ñóòè, ñòàâèëè ïîä ñîìíåíèå êîíöåïöèþ Êàíòîðà, òåîðåòèêî-ìíîæåñòâåííîå îáîñíîâàíèå ìàòåìàòèêè è ðÿä êîíêðåòíûõ ðåçóëüòàòîâ êëàññè÷åñêèõ ìàòåìàòè÷åñêèõ òåîðèé.
Íîâîå â ïîñòàíîâêå ïðîáëåìû ñóùåñòâîâàíèÿ â ìàòåìàòèêå íà÷àëà ÕÕ âåêà ñîñòîÿëî â òîì, ÷òî ýòà ïðîáëåìà ìíîãî øèðå è ãëóáæå, ÷åì ðàíüøå, çàõâàòèëà îñíîâíûå âîïðîñû îáîñíîâàíèÿ ìàòåìàòèêè è ëîãèêè è îêàçàëàñü òåñíî ñâÿçàííîé è ñ ôèëîñîôèåé.
È. Í. Áóðîâà. Ïàðàäîêñû òåîðèè ìíîæåñòâ è äèàëåêòèê.
À. Í. Êîëìîãîðîâ. Ìàòåìàòèêà â å¸ èñòîðè÷åñêîì ðàçâèòèè.
Ìàòåìàòè÷åñêàÿ ýíöèêëîïåäèÿ.
Â. Í. Ìîëîäøèé. Î÷åðêè ïî ôèëîñîôñêèì âîïðîñàì ìàòåìàòèêè.
Ã. È. Ðóçàâèí. Î ïðèðîäå ìàòåìàòè÷åñêîãî çíàíèÿ.
Ôèëîñîôñêèå ïðîáëåìû åñòåñòâîçíàíèÿ. Ïîä ðåä. Ñ. Ò. Ìèëþõèíà.
È. Ç. Öåõìèñòðî. Äèàëåêòèêà ìíîæåñòâåííîãî è åäèíîãî.
Ñ. À. ßíîâñêàÿ. Ìåòîäîëîãè÷åñêèå ïðîáëåìû íàóêè.
|



 Ðèñ. 1
Ðèñ. 1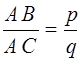 , ãäå ð
è q
— íàòóðàëüíûå ÷èñëà. Äðîáü
, ãäå ð
è q
— íàòóðàëüíûå ÷èñëà. Äðîáü 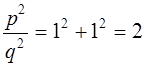 ;
; 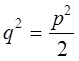 ,
,  Ðèñ. 2
Ðèñ. 2 .
. 

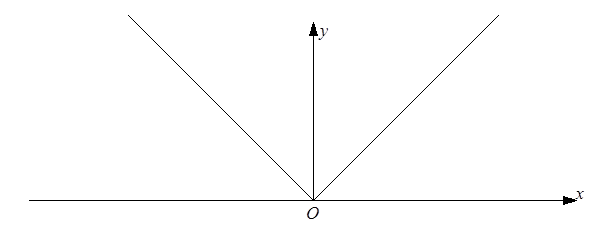
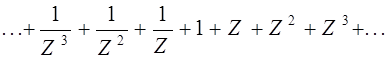
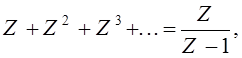
 ,
,  .
.  êàê ïðåäåëà èíòåãðàëüíîé ñóììû ñòîëêíóëîñü ñ ìíîãèìè òðóäíîñòÿìè. Åñòåñòâåííî, ÷òî ýòî îáñòîÿòåëüñòâî óêðåïëåíèþ òî÷êè çðåíèÿ Ëåéáíèöà íå ñïîñîáñòâîâàëî.
êàê ïðåäåëà èíòåãðàëüíîé ñóììû ñòîëêíóëîñü ñ ìíîãèìè òðóäíîñòÿìè. Åñòåñòâåííî, ÷òî ýòî îáñòîÿòåëüñòâî óêðåïëåíèþ òî÷êè çðåíèÿ Ëåéáíèöà íå ñïîñîáñòâîâàëî.  , äëÿ êîòîðîé ìîæíî ñîñòàâèòü ðÿä Ìàêëîðåíà, ñõîäÿùèéñÿ ïðè âñÿêîì õ
, íî êîòîðûé ñõîäèòñÿ âñþäó ê íóëþ, à íå ê ýòîé ôóíêöèè.
, äëÿ êîòîðîé ìîæíî ñîñòàâèòü ðÿä Ìàêëîðåíà, ñõîäÿùèéñÿ ïðè âñÿêîì õ
, íî êîòîðûé ñõîäèòñÿ âñþäó ê íóëþ, à íå ê ýòîé ôóíêöèè.